آموزش روش AHP فازی چانگ (FAHP)
تئوری فازی
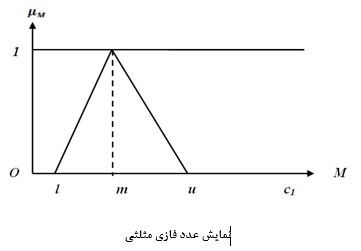
تئوری فازی در مقابل تئوری قطعی (سفید) اولین بار توسط زاده در سال 1965 ارائه شد و اعداد فازی بیان شد هدف در تئوری فازی حذف و بی اثر کردن ابهامات کلامی بود. ابهام و عدم قطعیت همیشه در تصمیم گیری ها وجود داشته است. اعداد فازی به دو صورت فازی مثلثی و فازی ذوزنقه ای بیان می شوند که پرکاربردترین آن ها فازی مثلثی است یک عدد فازی مثلثی به صورت زیر نمایش داده می شود.
اعداد فازی مثلثی بهصورت (l,m,u) ارائه میشود .که پارامترهای m ,l و u به ترتیب کوچکترین مقدار ممکن مورد انتظار ،مقدار محتملتر مورد انتظار و بیشترین مقدار ممکن مورد انتظار میباشند .هر عدد فازی مثلثی بهصورت نمایش خطی از طرف راست و چپش بهمنظور تابع عضویتش میتوانیم بهصورت زیر تعریف کنیم:
اعمال ریاضی بر روی اعداد فازی در معادلات زیر آورده شده است:
نکته: عمل تفریق و تقسیم فازی توجه بیشتری شود.
| عمل جمع اعداد فازی | (L1,M1,U1) + (L2,M2,U2)= (L1+L2,M1+M2,U1+U2) |
| عمل ضرب اعداد فازی |
(L1,M1,U1) *(L2,M2,U2)= (L1L2,M1M2,U1U2) |
| برای هر عدد حقیقی K | k(L1,M1,U1) = (kL1,kM1,kU1) |
| عمل تفریق اعداد فازی مثلثی | (L1,M1,U1) – (L2,M2,U2)= (L1-U2,M1-M2,U2-L1) |
| عمل تقسیم اعداد فازی مثلثی | (L1,M1,U1) / (L2,M2,U2)= (L1/U2,M1/M2,U2/L1) |
در ویدیوی زیر مفاهیم منطق فازی و روش AHP فازی چانگ گفته شده است پیشنهاد می شود حتما این ویدیو را ببینید.
توسعه و تعمیم تئوری فازی
بسیاری از سازه های ریاضی شبیه به یا کلی تر از مجموعه های فازی هستند. از آنجا که مجموعه های فازی در سال 1965 معرفی شدند ، بسیاری از سازه ها و تئوری های جدید ریاضی برای درمان عدم دقت ، عدم انعطاف پذیری ، ابهام و عدم اطمینان ساخته شده اند. برخی از این سازه ها و تئوری ها الحاق نظریه مجموعه فازی هستند ، در حالی که برخی دیگر سعی می کنند از لحاظ ریاضی از عدم دقت و عدم اطمینان به روشی متفاوت الگو بگیرند (بورژین و چونیحین 1997 ؛ کِر 2001 ؛ دسریجور و کر ، 2003).
تنوع چنین سازه ها و نظریه های مربوطه شامل موارد زیر است:
- intuitionistic fuzzy rough sets (Cornelis, De Cock and Kerre, 2003
- blurry sets (Smith, 2004)
- L-fuzzy rough sets (Radzikowska and Kerre, 2004,
- generalized rough fuzzy sets (Feng, 2010)
- rough intuitionistic fuzzy sets (Thomas and Nair, 2011,
- soft rough fuzzy sets (Meng, Zhang and Qin, 2011
- soft fuzzy rough sets (Meng, Zhang and Qin, 2011
- mathematics of partial presence (Baruah, 2012
- soft multisets (Alkhazaleh, Salleh and Hassan, 2011
- fuzzy soft multisets (Alkhazaleh and Salleh, 2012
مفهوم فازی
پروفسور لطفی زاده بنيانگذار تفکر فازی با ارائه مقاله مجموعه های فازی در سال 1965 ارائه داد از ویژگی های مفهوم فازی می توان به موارد زیر اشاره نمود.
- عدم پذيرش اوليه در مجامع علمی
- توسعه روزافزون کاربردها
- گسترش تفکر فازی، برگزاری کنفرانس های بين المللی و ارائه مقالات فراوان
- عدم قطعيت در برابر قطعيت
- گزاره های چندارزشی در برابر دوارزشی
- دقت بالا در برابر دقت کم
منطق فازی براساس این مشاهدات استوار است که افراد تصمیم می گیرند براساس اطلاعات نادرست و غیر عددی تصمیم گیری کنند. مدلها یا مجموعه های فازی وسیله ریاضی برای نشان دادن اطلاعات مبهم و نادرست است. این مدل ها قابلیت شناسایی ، بازنمایی ، دستکاری ، تفسیر و استفاده از داده ها و اطلاعات مبهم و فاقد اطمینان را دارند.
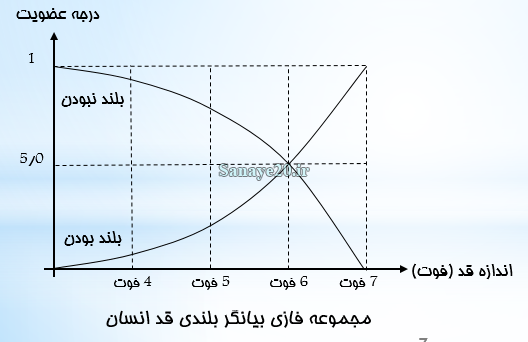
در شکل زیر مفهوم فازی بلند بودن قد یک انسان نشان داده شده است که نشان می دهد هر قدی با یک درجه عضویت بلند بود یا نبودن را در پی دارد.
روش فرایند سلسله مراتبی فازی (AHP فازی)
ضرورت فرایند تحلیل سلسله مراتبی فازی: روش AHP به طور گسترده در انتخاب یک گزینه از بین سایر گزینه ها استفاده شده است، اما در این روش مقایسات زوجی برای هر سطح با توجه به هدف انتخاب بهترین گزینه با استفاده از مقیاس نه تایی انجام می شود؛ بنابراین بکارگیری AHP ساعتی دارای کمبودهایی است، مانند اینکه روش AHP (1) اساسا در تصمیم گیری های crisp استفاده شده است (۲) مقیاس خیلی نامتعادل قضاوت را مورد بررسی قرار می دهد (۳) عدم اطمینان های موجود در قضاوت های فردی را در نظر نمی گیرد، همچنین (4) رتبه بندی این روش تقریبا غیردقیق است. (5) قضاوت های ذهنی، انتخاب و عملکرد تصمیم گیران تأثیرات بسیار زیادی در نتایج AHP دارد بعلاوه این موضوع که ارزیابی های افراد از شاخص های کیفی همیشه ذهنی و بنابراین غیردقیق هستند، موضوعی قابل قبول است. بنابراین AHP متعارف و کلاسیک، در دستیابی دقیق نیازمندیهای تصمیم گیران ناکافی و ناکارآمد به نظر می رسد. به منظور مدل سازی این نوع از عدم اطمینان ها در ترجیحات افراد بشر، تئوری مجموعه های فازی می بایست با مقایسات زوجی- به عنوان توسعه تکنیک AHP- ترکیب شود. این تکنیک تصمیم گیری ترکیبی درک دقیق تری از فرآیند تصمیم گیری ارائه می دهد.
AHP ابزاری برای تصمیم گیری چند معیاره است که می تواند مسائل پیچیده را به صورت سلسله مراتبی ایجاد کند ، در نتیجه ارزیابی همه معیارهای مرتبط با تصمیمی را که باید داده شود ساده می کند (Saaty، 1980). همه گزینه ها بر اساس هر معیار با استفاده از مقیاس ترجیحی به طور جداگانه مقایسه می شوند و برای هر معیار یک لیست اولویت از گزینه ها بدست می آید. مقیاس ترجیحی که بیشتر استفاده می شود مقیاس 1-9 است. AHP فازی ، تحلیلگر تصمیم گیری را قادر می سازد برای مواردی که بسیاری از عدم قطعیت ها در آن وجود دارد ، امتیاز واقعی تری برای گزینه های دیگر ارائه دهد. مدل تحليل توسعه چانگ (1992) يكي از آنهاست كه بستگي به ميزان احتمال هر معيار دارد.
از اعداد فازی مثلثی (l ، m ، u) برای ایجاد مقیاس مقایسه زوجی استفاده می شود و یک ماتریس مقایسه زوجی برای هر سطح در سلسله مراتب ساخته می شود. سپس ، زیر مجموعه های هر سطر در ماتریس محاسبه می شود تا یک مجموعه جدید داشته باشد. مقادیر کلی فازی مثلثی (لی ، mi ، ui) برای معیار Mi با محاسبه Li / Σ li ، mi / Σ mi ، ui / Σ ui ، (i = 1،2 ،… ، n) بدست می آید. توابع عضویت ، که به معنی میانگین وزن متناظر گزینه ها در ماتریس مربوطه است ، با استفاده از این مقادیر برای هر معیار محاسبه می شود. آنها نرمال شده و وزن نهایی اهمیت هر یک از معیارها به دست می آید.
برای اعمال فرایند بسته به این سلسله مراتب ، طبق روش تحلیل توسعه چانگ (1992) ، هر معیار در نظر گرفته می شود و برای هر معیار ، معیار gi اندازه گیری می شود.
از روش فرایند سلسله مراتبی فازی برای وزن دهی و رتبه بندی معیارها و یا گزینه های پژوهش استفاده می شود برای محاسبه اوزان در روش AHP فازی سه روش وجود دارد 1- روش آنالیز توسعه چانگ ، 2- روش بهبود یافته AHP فازی ، 3- روش اولویت بندی فازی میخایلو
در این بخش ما به توضیح روش AHP فازی بر اساس رویکرد آنالیز توسعه چانگ میپردازیم.
گام 1- تشکیل مدل سلسه مراتبی پژوهش
در این گام بعد از شناسایی معیارها، زیرمعیارها و گزینه های پژوهش باید مدل سلسله مراتبی پژوهش مشخص گردد.
گام 2- تشکیل جداول مقایسات زوجی و پاسخگویی بر اساس طیف زیر
در این گام همانند روش AHP باید مقایسات زوجی را ایجاد کرد و بر اساس طیف فازی زیر به این مقایسات زوجی پاسخ داد. این طیف 9 تایی AHP فازی است البته میتوان از طیف های 5 تایی و یا 7 تایی نیز استفاده نمود اما این طیف 9 تایی یک طیف استاندارد می باشد.
گام 3- محاسبه نرخ ناسازگاری مقایسات زوجی
در این گام باید نرخ ناسازگاری مقایسات زوجی بررسی شود و چنانچه این نرخ کمتر از 0.1 باشد یعنی مقایسه زوجی از ثبات و سازگاری مناسب برخوردار است. نرخ ناسازگاری در ماتریس های فازی به دو روش می توان محاسبه کرد اول این که ماتریس مقایسه زوجی فازی را دیفازی کرد و سپس نرخ ناسازگاری آن را به صورت قطعی محاسبه نمود و یا از روش محاسبه نرخ ناسازگاری به روش گوس و بوچر محاسبه نمود آموزش محاسبه نرخ ناسازگاری گوس و بوچر در این سایت موجود می باشد که با سرچ می توانید آموزش آن را به رایگان فرابگیرید.
گام 4- ادغام مقایسات زوجی
هنگامی که چندین پاسخ دهنده به مقایسات زوجی پاسخ داده اند برای ادغام آنها از روش میانگین هندسی استفاده می شود. تا یک ماتریس مقایسه زوجی ادغام شده حاصل شود. ادغام ماتریس های فازی به این صورت است که درایه های اول همه مقایسات با هم میانگین هندسی، درایه های دوم نیز با هم و درایه های سوم نیز با هم میانگین هندسی می گیریم.
گام 5- محاسبه اوزان با روش آنالیز توسعه چانگ
ابتدا بر اساس رابطه زیر مقادیر Si را برای هر سطر ماتریس مقایسه زوجی فازی بدست می آوریم.
که در آن gi مجموعه هدف است، و M gi j اعداد فازی مثلثی هستند. سپس بر اساس رابطه زیر میزان بزرگی (درجه ارجحیت) هر Si بر Sk را بدست می آوریم.
در مرحله آخر نیز با استفاده از رابطه زیر وزن های خام محاسبه می شوند که با تقسیم هر وزن خام بر مجموع اوزان خام، وزن نرمال حاصل می گردد.
مثال آنالیز توسعه چانگ
در این مثال فرض میکنیم سه معیار داریم و قصد داریم با استفاده از روش آنالیز توسعه چانگ اوزان معیارها را حساب کنیم
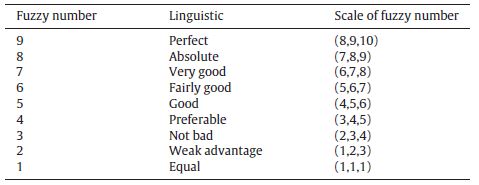
ابتدا مقایسات زوجی معیارها را انجام میدهیم و اوزان را محاسبه میکنیم سپس مقایسه زوجی زیرمعیارهای هر معیار را تشکیل داده و وزن زیرمعیارها نیز محاسبه می شود. در این پژوهش جهت محاسبه وزن در مقایسات زوجی، از عبارات کلامی و اعداد فازی مثلثی مندرج در جدول 1 استفاده شده است.
جدول 1: عبارات کلامی و اعداد فازی جهت وزن دهی به معیارها
| کد | اولویت ها | معادل فازی اولویت ها | ||
| حد پایین (L) | حد متوسط (m) | حد بالا (u) | ||
| 1 | اهمیت یکسان | 1 | 1 | 1 |
| 2 | یکسان تا نسبتا مهمتر | 1 | 2 | 3 |
| 3 | نسبتا مهم تر | 2 | 3 | 4 |
| 4 | نسبتا مهمتر تا اهمیت زیاد | 3 | 4 | 5 |
| 5 | اهمیت زیاد | 4 | 5 | 6 |
| 6 | اهمیت زیاد تا بسیار زیاد | 5 | 6 | 7 |
| 7 | اهمیت بسیار زیاد | 6 | 7 | 8 |
| 8 | بسیار زیاد تا کاملا مهمتر | 7 | 8 | 9 |
| 9 | کاملا مهمتر | 8 | 9 | 10 |
مقایسات زوجی معیارهای اصلی نسبت به هدف
گام 1- تشکیل ماتریس تصمیم ادغام شده
تعداد پاسخ دهندگان در این پژوهش 15 نفر میباشند که ماتریس ادغام شده مقایسات زوجی به صورت جدول 2 می باشد.
جدول 2: مقایسه زوجی معیارها نسبت به هدف (نرخ ناسازگاری: 0.023)
| C1 | C2 | C3 | |
| C1 | (1,1,1) | (0.643,0.912,1.298) | (1.294,1.604,2.013) |
| C2 | (0.77,1.097,1.555) | (1,1,1) | (0.81,1.122,1.561) |
| C3 | (0.497,0.623,0.773) | (0.64,0.891,1.234) | (1,1,1) |
گام2- برای محاسبه وزن این جدول از روش آنالیز توسعه چانگ استفاده شده است. نتایج این روش بهترتیب در زیر ارائه شده است. همانطور که در روند الگوریتم این روش بیان شد، ابتدا اعداد فازی هر سطر با هم جمع شده است. در زیر هر سطر یک عدد فازی را بیان میکند.
| 2.938 | 3.516 | 4.311 |
| 2.581 | 3.219 | 4.116 |
| 2.137 | 2.515 | 3.007 |
در قدم بعدی، تمام اعدادی که در مرحله قبل بدست آمدند با هم جمع میشوند و سپس معکوس خواهد شد. در واقع، در این مرحله تمام اعداد فازی را با هم جمع و سپس معکوس خواهد شد. این حاصل در زیر ارائه شده است.
(7.656,9.249,11.433)
در ادامه، این معکوس در تک تک سطرهای قدم اول (مجموع هر سطر) ضرب میشود تا مقادیر ادغامی نرمالایز شده هر سطر بدست آید. که این اعداد همان ها میباشند.
| 0.257 | 0.380 | 0.563 |
| 0.226 | 0.348 | 0.538 |
| 0.187 | 0.272 | 0.393 |
حال بایستی هر یک از سطرها نسبت به سطرهای زیرین خود مقایسه شوند. برای مقایسه هر سطر نسبت به خود، عدد یک را اختصاص میدهیم. مقادیر این مقایسات در زیر آمده است.
| 1.000 | 1.000 |
| 0.897 | 1.000 |
| 0.556 | 0.687 |
حال اوزان نهایی را از قدم قبل استخراج میکنیم. اوزان نهایی هر عامل برابر است با کمینه هر سطر. مقادیر اوزان خام و نرمالایزه شده در جدول 3 آورده شده است. وزن نرمال شده برابر است با تقسیم هر وزن خام بر مجموع اوزان خام.
جدول 3: اوزان نهایی معیارها
| معیار | اوزان خام | اوزان نرمالایز شده |
| C1 | 1.000 | 0.407 |
| C2 | 0.897 | 0.366 |
| C3 | 0.556 | 0.227 |
جهت دانلود آموزش کامل روش AHP فازی (FAHP) از طریق لینک زیر اقدام کنید این آموزش به صورت فیلم و زبان فارسی تهیه شده است. روش AHP فازی از روشهای تصمیم گیری چند شاخصه (MADM) میباشد که زیر مجموعه روش تصمیم گیری چند معیاره است. در آموزش های قبل به بررسی روش AHP فازی بهبود یافته پرداخته بودیم و امروز نیز این آموزش که بر اساس روش آنالیز توسعه چانگ که به تحلیل سلسله مراتبی فازی چانگ معروف است در نرم افزار متلب (matlab) تهیه شده است. کافیست کد متلب روش AHP فازی (Fuzzy AHP) را باز کنید و فقط مقایسات زوجی را به عنوان ورودی به نرم افزار دهید به صورت خودکار وزن هر چه تعداد معیار داشته باشید محاسبه میکند. این کد به صورتی نوشته شده است که محدودیتی در تعداد معیارها نیست. همچنین با ذکر یک مثال از این روش گام به گام آموزش داده شده است.
اگر نیازمند مشاوره در انجام پروژه های خود هستید با ما تماس بگیرید 09338859181
قسمتی از ویدیوی آموزش این:
جهت تهیه آموزش روش AHP فازی چانگ اینجا را کلیک کنید.
جهت تهیه آموزش روش AHP فازی چانگ اینجا را کلیک کنید.

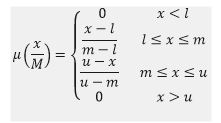
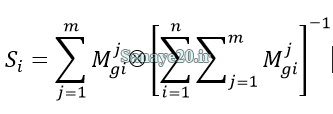
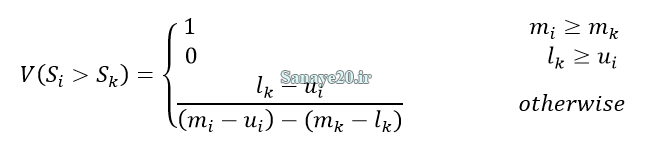
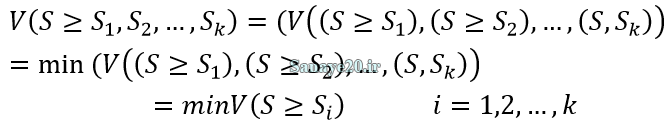
با سلام. هر عدد قطعی را به عنوان عدد فازی مثلثی با پهنای چپ و راست صفر در نظر میگیریم. چرا روش ahp فازی (crisp) و ahp غیر فازی به نتیجه واحد منجر نمیشوند؟؟
سلام. متوجه منظورتون نشدم
ممنون از اموزش های خیلی خوبتون .
در روش ahp ما یه فرمول برای محاسبه تعداد ماتریس های مقایسه زوجی داشتیم. برای ahp فازی تنها یک ماتریس مقایسه زوجی داریم؟؟
سلام. تعداد مقایسات زوجی در روش ahp چه فازی، چه ساده و چه هر محیط دیگه همگی از یک فرمول طبعیت میکنن (n*n-1/2)