دانلود رایگان کدهای متلب الگوریتم های فراابتکاری
در این مجموعه کد متلب (MATLAB) 20 الگوریتم فراابتکاری به صورت کاملا رایگان قرار داده شده است. که شامل کد متلب الگوریتم ژنتیک، الگوریتم PSO، الگوریتم خفاش، الگوریتم کرم شب تاب و… می باشد. لیست این مجموعه در زیر آورده شده است. الگوریتم های فراابتکاری برای حل مسائل بهینه سازی که با تکنیک های حل دقیق قابل محاسبه نیستند انجام می گیرد به دلیل اینکه بیشتر مسائل دنیای واقعی در ابعاد بزرگ می باشد بنابراین برای حل مدل آن ها تکنیک های فراابتکاری پیشنهاد می شود.
- الگوریتم کلونی زنبور عسل مصنوعی (Artificial Bee Colony)
- الگوریتم خفاش (Bat Algorithm)
- الگوریتم بهینه سازی جفرافیای زیستی (Biogeography Based Optimization)
- الگوریتم بهینه سازی فاخته (Cuckoo Optomization Algorithm)
- الگوریتم تکاملی تفاضلی (Differential Evolution Revised)
- الگوریتم کرم شب تاب (Firefly Algorithm)
- الگوریتم ژنتیک (Genetic Algorithm)
- الگوریتم جستجوی گرانشی (Gravitational Search algorithm)
- الگوریتم بهینه سازی گرگ خاکستری (Grey Wolf Optimizer)
- الگوریتم جستجوی هارمونی (Harmony search)
- الگوریتم رقابت استعماری (Imperialist Competitive Algorithm)
- الگوریتم بهینه سازی علف های هرز (Invasive Weed Optimization)
- الگوریتم لیگ قهرمانان (League Championship Algorithm)
- الگوریتم بهینه سازی مبتنی بر اپتیک (Optics Inspired Optimization)
- الگوریتم PSO بهینه سازی ازدحام ذرات (Particle Swarm Optimization)
- الگوریتم جهش قورباغه (Shuffled Frog Leaping Algorithm)
- الگوریتم جستجوی فراکتال تصادفی (Stochastic Fractal Search)
- الگوریتم مبتنی بر آموزش و یادگیری (Teaching Learning Based Optimization)
- الگوریتم بهینه سازی باد (Wind Driven Optimization)
- الگوریتم فراابتکاری عنکبوت اجتماعی (social spider algorithm)
تکنیک های فراابتکاری
اکثر مسائل دنیای واقعی، پیچیدگی بالا، محدودیت های غیرخطی، متغیرهای بهم وابسته و گستره وسیعی از راه حل ها را دارند. این مسئله، کاربرد تکنیکی با قابلیت حل مسائل بهینه سازی پیچیده در زمان واقعی را تضمین می کند. الگوریتم های فراابتکاری یکی از این تکنیک ها هستند. این الگوریتم ها روش هایی برای بهینه سازی می باشند که راه حل های منطقی و خوبی را طی مدت زمانی معقول ارائه می دهند. بهینه سازی یعنی با توجه به محدودیت های اعمال شده، به مجموعه ای از متغیرهای با ارزش جهت رسیدن به هدف حداقل سازی (حداکثرسازی) موضوع تابع هدف، دست یابیم، تقریبا در تمامی جنبه های زندگی، اعم از زندگی روزمره و برنامه ریزی برای کسب و کار و امور مالی و از کنترل صنعتی تا مهندسی طراحی، بصورت ذاتی نیاز به بهینه سازی است.
سیاری از مسائل بهینه سازی مهندسی معمولاً بسیار مشکل است و بسیاری از برنامه ها باید با این مسائل پیچیده روبرو شوند. در این مسائل، فضای جستجو با اندازه مسئله به صورت نمایی رشد می کند. بنابراین ، روشهای بهینه سازی سنتی راه حل مناسبی برای آنها ارائه نمی دهد. از این رو ، طی چند دهه گذشته ، الگوریتم های فرا ابتکاری بسیاری برای حل چنین مسائلی طراحی شده اند. محققان عملکرد خوبی از الگوریتم های فرا ابتکاری در طیف گسترده ای از مسائل پیچیده مانند مسائل برنامه ریزی، خوشه بندی داده ها، پردازش تصویر و فیلم ، تنظیم شبکه های عصبی و تشخیص الگوی نشان داده شده اند.
فرایند بهینه سازی
مفهوم بهینه سازی بدین صورت است که در بین پارامترهای یک تابع به دنبال مقادیری باشیم که تابع را کمینه یا بیشینه نماید. کلیه مقادیر مناسب جهت این امر را، راه حل های ممکن و بهترین مقدار از این مقادیر را، راه حل بهینه می نامند. الگوریتم های بهینه سازی هر دو نوع مسائل بیشینه سازی و کمینه سازی را پوشش می دهند. بهینه سازی کاربردهای زیادی در زمینه تخصیص منابع، زمان بندیها، تصمیم گیری ها و … را دارد . بهینه سازی همواره با مشکلات فراوانی همراه بوده است. شیوه های سابق برای حل کردن مشکلات بهینه سازی، مستلزم تلاش های محاسباتی بیشماری می باشد. الگوریتم های فراابتکاری تا حدی این مشکل را حل نموده اند. توسط این الگوریتم ها راه حل هایی پیدا می شوند که تقریبا به جواب بهینه نزدیکند.
طبقه بندی های مختلفی برای مدل های بهینه سازی ارائه شده است که از میان آنها یک طبقه بندی، طبقه بندی نالیی(۲۰۰۹) است که مدلهای بهینه سازی را به چهار دسته زیر تقسیم نموده است
- مدل های برنامه نویسی ریاضی
- مدل های بهینه سازی ترکیبی
- مدل های رضایت محدود
- مدل های نانولایتیک
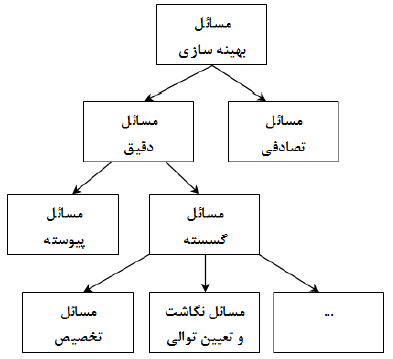
برای مثال، مسئله مسیریابی خودرو یک نوع از مسائل بهینه سازی ترکیبی است که ریشه در تجزیه و تحلیل ترکیبی دارد. لاولر، تعریف مناسبی برای تجزیه و تحلیل ترکیبی ارائه داده است. طبق تعریف وی تجزیه و تحلیل ترکیبی، مطالعه ریاضی محور از چیدمان، گروہ بندی، سفارش و یا انتخاب اشیای گسسته، معمولا در تعداد محدود است. بنابراین بهینه سازی ترکیبی می تواند به عنوان عمل جستجو برای یافتن بهترین تدابیر، بهترین گروه بندی و سفارش دهی و انتخاب تعریف شود شکل زیر یک طبقه بندی ابتدایی و تاحدودی ساده از مسائل بهینه سازی است. مسائل بهینه سازی در ابتدا به دو دسته قطعی (دقیق) و تصادفی تقسیم میشوند. مسائل دقیق نیز شامل دو دسته مسائل پیوسته و گسسته می باشند.
مسائل تصادفی دارای نوعی عدم قطعیت در هدف، محدودیت ها یا متغیرهای تصمیم هستند. این مفهوم از تصادفی به معنی عناصر تصادفی (Random) در روش تحقیق نیستند. این طبقه بندی مبتنی بر مشخصه های مسئله است. در مقابل، در مسائل دقیق هیچ عنصری با عدم قطعیت ندارد. معیار مهم دوم برای تقسیم بندی، مسائل پیوسته و گسسته هستند. مسائل پیوسته شامل متغیرهای تصمیم با ارزش های واقعی در هدف، محدودیت هایا هر دو مورد هستند در حالیکه مسائل گسسته مقادیر کاملا گسسته ای دارند که در بسیاری از موارد منتج به راه حل های شمارشی می گردند. مسائل گسسته شامل تقسیم بندی های بیشتری از جمله مسائل تخصيص و مسائل توالی و … می باشند. باید به این موضوع توجه داشته باشیم که مسائل زمان بندی و مسیریابی، زیر گروه مسائل نگاشت و توالی هستند.
با توجه به بررسی های صورت گرفته، تاکنون موفق ترین راه برای حل مسائل بهینه سازی، استفاده از تکنیکهای فراابتکاری می باشد. تکنیکهای فراابتکاری روش هایی تقریبی هستند که راه حل های خوب در مدت زمان قابل قبول ارائه می دهند، اما متضمن راه حل بهینه نیستند. یک اصل اساسی در تکنیک های فراابتکاری، هدایت عوامل مسئله ای خاص به سوی یک فضای عمومی و ارائه الگویی برای جستجوی راه حل بهینه است. ممکن است فضای جستجو برای پیمایشی جامع، در
برخی از مناطق بیش از حد بزرگ باشد و به بازرسی نیاز داشته باشد. این مسئله مربوط به تنوع و تشدید مسائل است و در طراحی فضای جستجوی تکنیکهای فراابتکاری نیاز به ایجاد تعادل و توازن بین این دو معیار متضاد می باشد. در شکل زیر این دو معیار در مقابل یکدیگر نشان داده شده اند. همچنین جوانب متفاوت دیگر فرابتكارات از جمله چگونگی تشخیص مناطق بهینه و میزان سرعت بررسی مناطق نیز موجود است.
یک سمت محور جستجوی محلی است که تعیین کننده جستجو در یک ناحیه باریک است و در سمت دیگر پیمایشی تصادفی در فضای جستجو است. تکنیکهای فراابتکاری مبتنی بریک جواب، در تلاشند تا جستجوی محلی را با ارئه الگوهای هدایتی جدا کرده و تکنیک های فراابتکاری مبتنی بر جمعیت نیز با معرفی تعدای راه حل، سعی در پوشش محدوده وسیع تری از فضای جستجو دارند .
بسیاری از الگوریتم های جستجوی معاصر برای بهینه سازی طراحی ، مبتنی بر ایده های اکتشافی تورینگ بوده اند. در حقیقت ، علاوه بر الگوریتم های ژنتیکی و شبکه های عصبی ، یک کلاس از الگوریتم های متاوریستیک وجود دارد که از برخی خصوصیات موفق سیستم های بیولوژیکی در طبیعت الهام گرفته شده است.
از طرف دیگر ، بسیاری از مسائل بهینه سازی طراحی در مهندسی و صنعت غیرخطی تحت محدودیت های سخت و در نتیجه اغلب NP-سخت هستند. بنابراین ، برای یافتن راه حل های بهینه برای چنین مسائل بهینه سازی ، معمولاً اگر غیرممکن باشد ، بسیار چالش برانگیز است.
در دو دهه گذشته ، ده ها الگوریتم جدید مانند بهینه سازی ذرات ذره ای ، تکامل دیفرانسیل ، الگوریتم های مورچه و زنبور ، جستجوی هماهنگی ، الگوریتم کرم شب تاب و جستجوی فاخته ظاهر شده اند و آنها پتانسیل بسیار خوبی در حل مسائل بهینه سازی مهندسی سخت ، خدمات تجارت الکترونیکی و مسائل داده کاوی نشان داده اند.
طبقه بندی تکنیک های فراابتکاری
راههای مختلفی برای طبقه بندی الگوریتم های فرابتکاری براساس ویژگیهای متمایز کننده آن وجود دارد. این روش ها عبارتند از:
1) الهام گرفته شده از طبیعت و بدون الهام از طبیعت: بسیاری از الگوریتم های فراابتکاری از طبیعت الهام گرفته شده اند، مانند الگوریتم ژنتیک و الگوریتم پرواز پرندگان. اما در مقابل، برخی از الگوریتم های فراابتکاری نیز از طبیعت الهام گرفته نشده اند. مانند الگوریتم جستجوی ممنوعه و یا الگوریتم جستجوی محلی تکراری (ILS).
2) مبتنی بر یک جواب و مبتنی بر جمعيت: الگوریتم های مبتنی بر یک جواب که روش های خط سهار نیز نامیده می شوند، در حین فرایند جستجو، یک جواب ارائه می دهند، در حالی که در الگوریتم های مبتنی بر جمعیت در حین جستجو، یک جمعیت از جواب ها در نظر گرفته می شوند. تکنیک های مبتنی بریک جواب (برای مثال TS ، SA و جستجوی محلی)، حالت تشدید داشته در حالی که تکنیکهای مبتنی بر جمعیت (همچون الگوریتم ژنتیک و پرواز پرندگان و …) بیشتر مبتنی بر کاوش در فضای جستجو هستند.
3) تکرار شونده و حریصانه: الگوریتم های تکرار شونده (مثل SA و PSO)، ازیک (یا یک مجموعه) راه حل آغاز شده و طی مراحل فرایند جستجو کنترل و اصلاح می گردد. الگوریتم حریصانه (مثل ACO) از یک راه حل تھی آغاز شده و در هر مرحله به متغیرهای تصمیم ارزشی یعنی همان ارزش افزوده اضافه شده به مجموعه راه حل، اختصاص می یابد. این الگوریتم بهترین انتخاب را با توجه به شرایط مسئله انجام می دهد، به امید آنکه با ادامه ی همین روش بهینه سازی انجام شود. البته این نکته که بهترین انتخاب فعلی ما را به جواب بهینه میرساند را باید اثبات کرد. در شیوه حریصانه در هر مرحله عنصری که بر مبنای معیاری معین بهترین» به نظر می رسد، بدون توجه به انتخاب هایی که قبلا انجام شده با در آینده انجام خواهد شد. انتخاب می گردد.
4) یک ساختار در مقابل چند ساختار همسایگی: اغلب فراابتکارات، روی یک ساختار همسایگی واحد عمل می کنند. به بیان دیگر، توپولوژی چشم انداز شایستگی در طی الگوریتم فراابتکاری تغییر نمی کند. فرا ابتکارات دیگر مانند جستجوی همسایگی متغیر(MNS)، مجموعه ای از ساختارهای همسایگی را به کار می گیرند که با عوض کردن چشم اندازهای شایستگی متفاوت، امکان متنوع سازی جستجو را فراهم می کنند
5) الگوریتم های با تابع هدف ایستا در مقابل پویا: در این روش فرابتکارات بر اساس نحوه استفاده از تابع هدف تقسیم بندی می شوند. در حالی که بعضی الگوریتم ها، تابع هدف داده شده در نمایش مسئله را به همان صورتی که هست نگه می دارند، بعضی دیگر مانند جستجوی محلی هدایت شده (کا)، در طول جستجو، آن را اصلاح می کنند. ایده این عمل، گریز از کمینه محلی از طریق اصلاح چشم انداز جستجو است. بر این اساس در طی جستجو، سعی می شود تابع هدف توسط به کار گیری اطلاعات جمع آوری شده در طی فرآیند جستجو، تغییر یابد.
یک مؤلفه مهم در متاهیورستیک مدرن، اکتشاف است ، غالباً استفاده از تصادفی سازی، یک الگوریتم را قادر می سازد تا توانایی پرش از هر بهینه محلی را برای کشف جستجو در سطح جهانی داشته باشد.
در صورت محدود بودن مراحل به یک منطقه محلی ، از تصادفی سازی نیز می توان برای جستجوی محلی در اطراف بهترین جریان استفاده کرد. وقتی مراحل بزرگ هستند ، تصادفی سازی می تواند فضای جستجو را در مقیاس جهانی کشف کند. تنظیم دقیق میزان صحیح تصادفی و متعادل کردن جستجوی محلی و جستجوی جهانی در کنترل عملکرد هر الگوریتم فراگرایی بسیار مهم است.
تکنیک های تصادفی سازی می تواند روشی بسیار ساده با استفاده از توزیع یکنواخت و یا توزیع های گاوسی یا روش های پیچیده تری به عنوان روش های مورد استفاده در شبیه سازی مونت کارلو باشد.
در جدول زیر کاربردهایی از انواع الگوریتم ها آورده شده است.
| الگوریتم | حوزه کاربردی |
| شبیه سازی تبرید (SA) |
برنامه ریزی جاب شاپ در سیستم های تولید مسیریابی در سیستم حمل ونقل طراحی شبکه تلفن همراه، مسیریابی، تخصیص کانال |
| جستجوی ممنوعه (TS) |
تخصیص منابع اصلی در صنعت مهندسی تکنولوژی، توزیع انرژی داده کاوی، دسته بندی |
| الگوریتم ژنتیک (GA) |
برنامه ریزی مالی، پیش بینی سهام پردازش تصویر ترتیب دهی در FMS |
| تکامل تفاضلی |
پردازش سیگنال و تصویر طراحی محصول مهندسی شیمی |
| بهینه سازی ازدحام ذرات (PSO) |
طراحی شبکه، مسیریابی شبکه عصبی شبیه سازی سیستم تصمیم گیری و برنامه ریزی |
| بهینه سازی کلونی مورچگان (ACO) |
پوشش و تقسیم بندی مجموعه حداکثر عدم وابستگی در مجموعه بسته بندی |
| الگوریتم ممتیک |
شبکه عصبی، طبقه بندی مهندسی سیستم برنامه ریزی تولید |
| سیستم های ایمنی مصنوعی (AIS) |
داده کاوی و تحلیل داده ها خوشه بندی و طبقه بندی امنیت کامپیوتر و شبکه |
مزایای الگوریتم های فراابتکاری
الگوریتم های فراابتکاری در دو دهه گذشته در زمینه بهینه سازی و همینطور مسائل NP سخت کاربرد بسیار وسیعی پیدا نمودند. روش های بهینه سازی سنتی به دلیل پیچیدگی مسائل و ابعاد مسائل، در ارائه نتایج رضایت بخش با شکست مواجه شدند. ویژگی های برجسته الگوریتم های فراایتکاری که باعث برتری آنها نسبت به روش های سنتی و تناسب بیشتر آنها با دنیای واقعی گردیده، در زیر ذکر شده اند.
- کاربرد عمومی
روش های دقیق و تکنیکهای فراابتکاری، روش هایی برای حل مسائل خاص می باشند. برای هر مسئله، نیاز به اعمال مکانیسم خاصی است. همچنین، یادگیری از یک بسته کاربردی، براحتی در دیگر مسائل قابل اعمال نیست. به هرحال در روشهای فراابتکاری به جای آغاز کار از ابتدا، باید تنها به انطباق الگوریتم با مستلهای خاص پرداخت.
- زمان محاسباتی معقول
الگوریتم های فراابتکاری حتی برای مسائلی با ساختارهای بسیار پیچیده نیز قادر به ارائه پاسخ های نزدیک به بهینه در مدت زمانی قابل قبول هستند. این الگوریتم ها به خوبی بین شدید و تنوع فضای جستجو، تعادل ایجاد می نمایند. به عنوان مثال برای حل مدل های مکان یابی مسیریابی که در طراحی سیستم های صنعتی استفاده می شود بکارگیری الگوریتم فراابتکاری باعث رسیدن به جواب در کمترین زمان ممکن می شود.
- يافتن بهينه جهانی
الگوریتم های بهینه سازی با مسائلی با چندین نقطه کمینه محلی نسبت به مسائل دقیق، که شانس بیشتری برای واقع شدن در نقطه بهینه محلی دارند، سازگار ترند. به هرحال الگوریتم های فرابتکاری محدودیت هایی دارند که در زیر آنها را ذکر می کنیم.
- الگوریتم های فراابتکاری متضمن راه حل بهینه نیستند
- اثبات کارایی الگوریتم ها از لحاظ تئوریک کار دشواری است. معمولا برای الیت کارایی آنها به نتایج تجربی اتکا می گردد
- هر الگوریتم فرایتکاری مزایا و محدودیت های مختص به خود را دارد که منجر به انطباق بیشتر آن با مسئله ای خاص می گردد
ترکیب الگوریتم ها
به طور کلی هدف از ایجاد روش های فراابتکاری ترکیبی، نوعی توانمندسازی متقابل این روش ها در اعمال راهبردهای مناسب در فرایند جستجو است؛ به نحوی که همپوشانی مفیدی در خصوص نقاط ضعف و قوت این روش ها محقق شده و رویکرد ترکیبی در مقایسه با اجرای مستقل این روش ها و حتی نسبت به سایر روش های بهینه سازی، کارایی قابل توجهی را ارائه دهد. لذا در یک جمع بندی می توان هدف از این رویکردهای ترکیبی را به سه موضوعی که در ادامه می آید، منسوب کر.
یک روش بسیار معمول، استفاده از روش های خط سیر در روش های مبتنی بر جمعیت است. دلیل این مسئله زمانی روشن می شود که نقاط قوت روش های خط سیر و مبتنی بر جمعیت مورد تحلیل فرار گیرد.
بسیاری از متاهیورستیک ها معمولاً می توانند دارای خصوصیات همگرایی جهانی باشند، بنابراین معمولاً در تعداد محدودی از تکرارها یا ارزیابی های عملکرد ، می توانند بهینه جهانی را در عمل بیابند. این مسئله باعث می شود که الگوریتم های متاهیورستیک برای حل بهینه سازی جهانی مناسب باشند.
قدرت روش های مبتنی بر جمعیت بر اساس مفهوم ترکیب مجدد راه حل ها برای رسیدن به راه حل های جدید است. در الگوریتمهای تکاملی و جستجوی پراکنده، ترکیب مجدد توسط یک یا چند عملگر ترکیب مجدد، به طور صریح انجام می شود. در روشی مانند ACO ترکیب مجدد، ضمنی است؛ چون راه حل های جدید با استفاده از یک توزیع روی فضای جستجو تولید می گردند که تابعی از جمعیت های قبلی است. این کار اجازه می دهد گام های هدایت شده در فضای جستجو برداشته شود که معمولا بزرگتر از گام های انجام شده با روش های خط سیر است. به بیان دیگر، راه حل حاصل از ترکیب مجدد در روش۔ های مبتنی بر جمعیت معمولأ نسبت به راه حل قبلی و بعدی که از اعمال یک جابه جایی به دست می آید متفاوت تر از والدین خود می باشند. جالب توجه است که در کلیه روشهای مبتنی بر جمعیت، رویه هایی وجود دارد که راه حل های خوب یافته شده در طی جستجو، به امید یافتن راه حل های بهتر، بر فرایند جستجو اثر می گذارند، این کار در اتصال مجدد مسیر به صریح ترین روش پیاده سازی می شود.
مؤلفه های اصلی، راه حل های راهنما هستند که راه حل های خوب بافته شده می باشند و به راه حل ها مقدار اولیه می دهند. راه حل های جدید با اعمال جابه جایی هایی برای کاهش فاصله بین راه حل حاصل و راه حل راهنما، تولید می گردند. در الگوریتم های تکاملی این کار با نگهداری بهترین (یا تعدادی از بهترین) | راه حل های بافته شده از زمان شروع اجرای الگوریتم در جمعیت، انجام می شود. این رویه، یک فرایند تکامل حالت پایدار نامیده میشود. در بعضی پیاده سازی های ACO ، زمان بندی به روز رسانی فرومون به نحوی انجام می شود که وقتی الگوریتم در حال همگرا شدن به یک راه حل است، فقط بهترین راه حل های یافته شده از ابتدای الگوریتم برای به روزرسانی آثار فرومون به کار می روند. این موضوع متناظر با تغییر جهت و هدایت فرایند جستجو به سمت یک راه حل خیلی خوب و به امید یافتن راه حل های بهتر در مسیر پیش رو می باشد.
قدرت روش های خط سیر در روش کاوش منطقه اميدبخش در فضای جستجو است. همان قدر که در این روش ها، جستجوی محلی یک مؤلفه پیش برنده است، یک منطقه امید بخش به روش ساخت یافتهتری از روشهای مبتنی بر جمعیت، جستجو می شود. از این طریق خطر گم کردن راه حل های خوب، در زمان نزدیک شدن به آنها، به اندازه روشهای مبتنی بر جمعیت بالا نیست.
در اصل ، برای اینکه یک الگوریتم فراابتکاری کارآمد باشد ، باید از قابلیت های ویژه ای برخوردار باشد. یكی از این موارد این است كه می توان راه حل های جدیدی تولید كرد كه معمولاً می تواند راه حل های قبلی / موجود را بهبود بخشد و همچنین بتواند مهمترین زمینه های جستجو را كه در آن ممكن است بهینه جهانی باشد ، پوشش دهد. قابلیت دیگر این است که یک الگوریتم باید بتواند از هرگونه بهینه محلی فرار کند و در حالت محلی نتواند گیر کند. یک ترکیب خوب ممکن است در شرایط مناسب به راندمان خوب منجر شود و این اغلب نیاز به متعادل کردن دو مؤلفه مهم هرگونه الگوریتم فراابتکاری دارد: قابلیت کشف و جستجوی بالا(exploration) و قابلیت استخراج کردن(exploitation). با این حال ، این خود یک کار بهینه سازی حل نشده است.
چنانچه این مطالب مفید بوده است لطفا امتیاز ستاره ای را در ابتدای پست وارد کنید