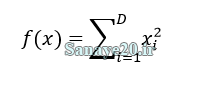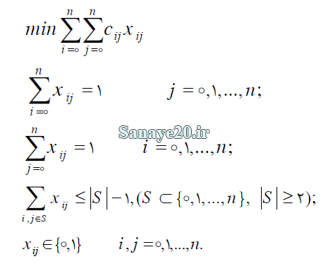الگوریتم جستجوی هارمونی و فروشنده دوره گرد
مقدمه
الگوریتم جستجوی هارمونی (Harmony search) از الگوریتم های معروف فراابتکاری است که بر اساس یک روش موسیقی ارائه شده است که برای حل مسائل بهینه سازی استفاده می گردد. در این مطلب ابتدا به توضیحات مسائل بهینه سازی و سپس توضیح الگوریتم جستجوی هارمونی پرداخته می شود. در انتها نیز برای سنجش عملکرد این الگوریتم از توابع بنچمارک استفاده می شود که در نرم افزار MATLAB این شبیه سازی صورت می گیرد و در قالب چند ویدیو نیز توضیح داده می شود. سپس مساله فروشنده دوره گرد (TSP) توسط این الگوریتم پیاده سازی می شود.
مسائل بهینه سازی
مهندسان و تصمیم گیرندگان، با مسایلی روبه رو هستند که پیچیدگی آنها روز به روز افزایش پیدا میکنند. این مسایل در زمینه های مختلفی نظیر تحقیق در عملیات، طراحی سیستم های مکانیکی، پردازش تصوير و الکترونیک به وجود می آیند. در اغلب این زمینه ها، می توان مسأله را به صورت یک مسأله بهینه سازی بیان کرد. در مسایل بهینه سازی، یک یا چند تابع هدف تعریف می شود که باید در عین حال که تمامی پارامترهای مسأله مورد توجه قرار می گیرند، کمینه یا بیشینه شود. معمولا در مسایل بهینه سازی محدودیت هایی نیز تعریف می شود. تمامی جواب های موجود، باید در این محدودیتها صدق کنند در غیر این صورت جوابها موجه نخواهند بود. تمامی جوابها بررسی و ارزیابی میشوند و بعد از بررسی مشخص میشود که همه درست و صادق بوده اند. مشخص کردن محدودیت ها گام مهمی در رسیدن به جواب هست.
فرض کنید هدف از حل مسأله ی بهینه سازی کمینه کردن تابع هدف (x) f باشد. همچنین فرض کنید مجموعه جواب های موجه با X نمایش داده شود. در این صورت مدل ریاضی مسألهی بهینه سازی را می توان به صورت زیر نوشت:
min f(x)
s.t. x∋X
مسائل بهینه سازی، از نظر نوع متغیرهای تصمیم می توانند به دو گروه مسایل گسسته و مسایل پیوسته تقسیم بندی شوند. در عمل ممکن است مسأله ای به صورت آمیخته تعریف شود که همزمان دارای متغیرهای گسسته و پیوسته باشد. هنگامی که متغیرهای تصمیم در مسایل بهینه سازی گسسته باشند، مسألهی یافتن جوابهای بهینه، بهینه سازی ترکیبی نامیده می شود.
پیچیدگی محاسباتی
یک الگوریتم برای حل مسأله، نیاز به دو منبع مهم دارد:
- زمان
- فضای حافظه
پیچیدگی زمانی یک الگوریتم، برابر تعداد گام های مورد نیاز برای حل یک مسأله با اندازه n است. پیچیدگی معمولا براساس بدترین حالت تعریف می شود. هدف از تعیین پیچیدگی محاسباتی یک الگوریتم یافتن تعداد دقیق گام های الگوریتم نیست، بلکه هدف یافتن یک کران بالا برای تعداد گام هاست. نماد O بزرگ، یکی از نمادهای رایج در تحلیل پیچیدگی الگوریتم ها است. مثلا وقتی می گوییم یک الگوریتم به اندازه (O f(n حافظه میگیرد، یعنی مقدار حافظه اشغال شده توسط الگوریتم، حداکثر به اندازه (f(n است که در آن f تابعی از ابعاد مسأله است.
یکی از مباحث مهم پیچیدگی محاسباتی، الگوریتم با زمان چند جمله ای است. بنا بر تعریف، یک الگوریتم، الگوریتم با زمان چند جمله ای است اگر پیچیدگی آن (O p(n باشد که در آن (n)p یک تابع چند جمله ای از n است. تعریف مهم دیگر در تحلیل پیچیدگی محاسباتی، الگوریتم با زمان نمایی است. یک الگوریتم در صورتی یک الگوریتم با زمان نمایی است که پیچیدگی آن O (cn) باشد که در آن c یک عدد حقیقی ثابت بزرگتر از یک است.
پیچیدگی محاسباتی مسایل
پیچیدگی محاسباتی یک مسأله، برابر است با پیچیدگی محاسباتی بهترین الگوریتمی که آن را حل میکند. یک مسأله، مسأله آسان نامیده می شود، اگر برای حل آن، یک الگوریتم با زمان چند جمله ای وجود داشته باشد. در مقابل، یک مسأله سخت نامیده می شود، اگر برای حل آن هیچ نوع الگوریتمی با زمان محاسباتی چند جمله ای وجود نداشته باشد. نظریه پیچیدگی مسایل، براساس مسایل تصمیم تعریف می شود. یک مسأله تصمیم، همیشه یک جواب «بلی» یا «خیر» دارد. هدف از مسایل بهینه سازی، پیدا کردن جواب بهینه است. هر مساله بهینه سازی، قابل تبدیل به یک مسأله تصمیم است.
از لحاظ پیچیدگی محاسباتی، مسایل تصمیم به دو کلاس مهم P و NP تقسیم می شوند. کلاس پیچیدگی P، شامل مجموعه ای از مسایل تصمیم است که می توانند در یک زمان محاسباتی چند جمله ای قطعی حل شوند. یک الگوریتم قطعی برای یک مسأله تصمیم، دارای زمان محاسباتی چند جمله ای است، اگر پیچیدگی بدترین حالت آن مسأله به وسیلهی یک تابع چند جمله ای (n)p محدود شده باشد، که در آن بر اندازه ورودی مسأله است، بنابراین یک مسأله P، قابل حل در زمان (O (nk است، که در آن به یک مقدار ثابت و n اندازه ورودی مسأله است. در نتیجه، برای حل هر یک از مسایل P، یک الگوریتم با زمان چند جمله ای وجود دارد. مسایل کوتاهترین مسیر، ماکزیمم جریان و مسایل بهینه سازی خطی از مسایل معروف این کلاس هستند.
کلاس پیچیدگی NP، شامل مجموعه ای از مسایل تصمیم است که می توان آنها را توسط الگوریتم های غیر قطعی چند جمله ای حل کرد. الگوریتم های غیر قطعی چند جمله ای، شامل الگوریتم های دو مرحله ای است. در مرحله اول، یک جواب کاندید به صورت تصادفی تولید می شود. این مرحله به صورت غیر قطعی است. در مرحله دوم، صحه گذاری جواب کاندید انجام می شود در صورتی که جواب کاندید بیان کنندهی یک جواب مساله باشد، مقدار «بله» و در غیر این صورت مقدار «خیر»، به عنوان جواب نهایی برای مساله تصمیم، برگردانده می شود. در این نوع الگوریتم های فاز دوم در یک زمان چند جمله ای انجام می شود، بنابراین غیر قطعی بودن الگوریتم مربوط به مرحله اول و زمان چند جمله ای مربوط به مرحله دوم الگوریتمها است.
مسایل NP -کامل، سخت ترین مسایل در بین مسایل NP هستند. کلاس NP -کامل، یعنی مسایل کامل، غیر قطعی با زمان چند جمله ای است. این مسایل قابل حل با الگوریتم های قطعی با زمان چند جمله ای نیستند.
کلاس دیگری از مسایل، مسایل NP- سخت هستند. برای حل مسایل NP – سخت، نیز الگوریتم های قطعی چند جمله ای وجود ندارد یا به عبارتی دیگر، زمان حل آنها با افزایش ابعاد مسأله، به صورت نمایی افزایش می یابد. هر مسأله در کلاس NP-کامل، یک مسأله NP – سخت به حساب می آید.
برخی از مسایل NP – سخت، عبارتند از:
- مسایل توالی و زمان بندی؛ نظير زمان بندی کارگاهی
- مسایل تخصیص و مکان یابی؛ نظير مسأله ی تخصیص تعمیم یافته و مکان یابی تسهیلات، مکان یابی هاب
- مسایل گروه بندی نظیر خوشه بندی، افرازبندی گراف
- مسایل مسیریابی و پوشش؛ نظير مسأله مسیریابی وسیله نقلیه، مسأله پوشش مجموعه.
روش های حل مسائل بهینه سازی
مسایل بهینه سازی به دو دسته ی مسائل بهینه سازی ترکیبی و پیوسته تقسیم بندی می شوند. در زمیندی مسایل پیوسته، روش های کلاسیک بسیاری برای یافتن بهیندی سراسری ارایه شده اند، اما این تکنیک ها در صورتی که تابع هدف دارای ویژگی های مشخصی (نظير محدب بودن) نباشد، معمولا کارایی ندارند. روشهای حل مسائل بهینه سازی پیوسته، به دو دسته روش های بهینه سازی خطی و غیر خطی تقسیم بندی می شوند. روش های حل مسائل بهینه سازی ترکیبی را نیز میتوان به دو قسمت الگوریتم های دقیق و الگوریتم های ابتکاری تقسیم بندی کرد. الگوریتم های دقیق برای حل مسائل بهینه سازی ترکیبی نظیر روش شاخه و کران، روش هایی هستند که رسیدن به جواب بهینه را تضمین می کنند. روش های دقیق، معمولا برای حل مسایل با اندازه های کوچک یا متوسط، می توانند به کار گرفته شوند. برای حل مسایل واقعی که معمولا با ابعاد بزرگ و پیچیده هستند امکان استفاده از روش های دقیق وجود ندارد، بنابراین اغلب از روش های ابتکاری استفاده میشود.
بیشتر مسائل بهینه سازی ترکیبی، در کلاس مسایل NP –سخت قرار می گیرند، بنابراین برای حل آنها باید از روش های تقریبی که جواب های نزدیک به بهینه را در زمانی قابل قبول به دست می آورند، استفاده کرد. الگوریتم هایی از این دست الگوریتم های ابتکاری نام دارند.
الگوریتم های ابتکاری، معمولا به دنبال رسیدن به جواب های خوب، یعنی جوابهای نزدیک به بهینه، در زمان محاسباتی قابل قبول هستند ولی قادر به تضمین بهینه بودن جواب های به دست آمده نیستند. روش های ابتکاری مختلفی برای حل مسائل بهینه سازی ترکیبی ابداع شده است که در آنها، جواب نزدیک به بهینه تولید میشود. مشکل این روشها، این است که اکثر آنها فقط در مورد یک مسألهی به خصوص کاربرد دارند.
الگوریتم های ابتکاری به انواع مختلفی تقسیم میشوند، که در ادامه به آنها اشاره می شود:
الگوریتم های سازنده
یک دسته از انواع الگوریتم های ابتکاری هستند، که در آن یک جواب از مسأله به تدریج و مرحله به مرحله با توجه به داده های مسأله ساخته می شود. مثلا الگوریتم نزدیک ترین همسایگی برای حل مسأله TSP یک الگوریتم سازنده است که در آن اولین شهر را به صورت تصادفی انتخاب کرده و سپس با توجه به ماتریس فاصله در هر تکرار نزدیک ترین شهر به مجموعه شهرهای عضو تور، انتخاب شده و به تور اضافه می شود. الگوریتم های سازنده بسیار سریع هستند، اما معمولا فاصله جواب تولید شده با جواب بهینه زیاد است.
الگوریتم های بهبود دهنده
از الگوریتم های بهبود دهنده، تحت عنوان الگوریتم های جستجوی محلی نیز یاد می شود. نوع دیگری از الگوریتم های ابتکاری هستند که در آنها معمولا جستجو از یک جواب اولیه شروع می شود. این جواب اولیه ممکن است به صورت تصادفی تولید شده باشد و یا اینکه با یک الگوریتم سازنده قبلا حاصل شده باشد. سپس با جستجوی موضعی در همسایه های این جواب، سعی در بهبود جواب دارند و این کار را به صورت بازگشتی در هر تکرار از الگوریتم انجام میدهند. ساختار همسایگی جواب های این نوع از الگوریتم ها بسیار مهم است. مثلا در الگوریتم همای تپه نوردی (برای مسایل ماکزیمم سازی) و گرادیان کاهشی (برای مسایل مینیمم سازی از ایده جستجوی محلی برای یافتن جوابهای بهتر در همسایگی جواب فعلی استفاده میکنند. اما مشکل اصلی این نوع از الگوریتم ها آن است که اغلب در دام بهینه محلی که نسبت به بهینه سراسری بسیار بدتر است، گرفتار می شوند.
الگوریتم های فراابتکاری
یک الگوریتم فراابتکاری، یک چارچوب الگوریتمی است که می تواند با تغییرهایی کم، برای مسائل بهینه سازی مختلف به کار رود. استفاده از الگوریتم های فراابتکاری، به طور قابل ملاحظه ای توانایی یافتن جواب های با کیفیت بالا را برای مسائل بهینه سازی ترکیبی افزایش می دهد. به عبارت دیگر، یک الگوریتم فراابتکاری، یک روش ابتکاری است که قادر به جستجوی فضای جواب، برای یافتن جواب های با کیفیت بالا است. هدف مشترک تمامی الگوریتم همای فراابتکاری، حل مسایلی است که به مسایل بهینه سازی سخت مشهور هستند. الگوریتم های فراابتکاری به عنوان الگوریتم های حل مسایل NP- سخت ارایه شده اند. این الگوریتم ها می توانند برای حل این گونه مسایل، یک جواب مناسب را در زمانی قابل قبول به دست آورند (منبع).
انتخاب و به کارگیری الگوریتم های فراابتکاری وابستگی شدیدی به شرایط مسأله مورد بحث، نوع متغیرها، گسترش و بزرگی مساله و شرایط و محیط به کارگیری آن دارد. یکی از عیب های این الگوریتم های تولید یک جواب یا تعداد محدودی از جوابها و توقف آنها در بهینه محلی با کیفیت پایین است. با استفاده از الگوریتم های فراابتکاری می توان این مشکلات و عیب های روش های ابتکاری را برطرف نمود. این الگوریتم ها، با معرفی اصول سیستماتیک برای خارج شدن از بهینه های محلی یا جلوگیری از قرار گرفتن در بهینه های محلی با این مشکل برخورد می کنند. ویژگی مشترک الگوریتم های فراابتکاری، استفاده از مکانیزم های خروج از بهینه محلی است. روش های فراابتکاری، دارای ویژگیهای مشترک زیر هستند:
- این روشها همگی، تا حدودی احتمالی هستند، چنین رویکردی، این امکان را میدهد که از قرار گرفتن در دام بهینه محلی جلوگیری شود.
- این روش ها معمولا برای حل مسایل گسسته ارایه شده اند، اما امکان کاربرد در مسایل پیوسته را نیز دارند.
- این روشها معمولا از مفاهیم زیست شناسی، رفتار شناسی جانوری و فیزیک الهام گرفته شده اند.
- یکی از عیب های مشترک در این روشها، دشوار بودن تنظیم و تطبیق پارامترها است.
از جمله الگوریتم های فراابتکاری معروف می توان به الگوریتم ژنتیک، الگوریتم PSO، الگوریتم جستجوی ممنوعه، الگوریتم جستجوی هارمونی اشاره نمود. هر کدام از الگوریتم های فوق دارای مراحل خاص به خود می باشند که در هر مساله ای کاربرد خاص خود را دارند.
الگوریتم جستجوی هارمونی
الگوریتم جستجوی هارمونی تاکنون برای مسایل بهینه سازی مختلف استفاده شده است. در این جا به معرفی جدیدترین کاربردهای الگوریتم جستجوی هارمونی پایه می پردازیم. کاربرد الگوریتم جستجوی هارمونی (HSA) در علوم مختلف و مسایل بهینه سازی فنی و مهندسی عبارت است از:
- کاربردها در دنیای واقعی: مسأله آهنگ سازی، جدول سودوكو، جدول زمان بندی، برنامه ریزی تور، حمل و نقل.
- مسایل علوم کامپیوتر: خوشه بندی صفحه وب، خلاصه سازی متن، مسیریابی اینترنت، ردیابی تصویری، رباتیک.
- مسایل مهندسی برق: پخش بار سامانه انرژی، تشخیص عکس الکترونیکی، طراحی سیستم های قدرت، بهینه سازی معکوس چند سطحی، شبکه تلفن همراه.
- مسایل مهندسی عمران: طراحی سازه، طراحی شبکه آب، برنامه ریزی سد، کالیبراسیون مدل سيل، مدیریت آبهای زیرزمینی، تجزیه تحلیل پایداری خاک، حفاظت از محیط زیست، مسیریابی وسیله ی نقلیه.
- مسایل مهندسی مکانیک: طراحی مبدل های حرارتی، طراحی لوله حرارتی ماهواره ای ، ساختار سازه های دریایی پهلوگیر.
- بیوگرافی و کاربردهای پزشکی: پیش بینی ساختار RNA، سمعک، فیزیک پزشکی.
در زیر شرح تفصیلی جزئیات الگوریتم جستجوی هارمونی (HSA) پایه و ارتباط آن با مفهوم موسیقیایی می پردازیم
بهینه سازی در زمینه های موسیقی
در بداهه نوازی موسیقی یک گروه از نوازندگان دانگهای صدا، از الات موسیقی خود را في البداهه و پی در پی به دنبال یک هماهنگی مطلوب و خوشایند می نوازند این همنوازی باید بر اساس استانداردهای صوتی و زیبایی موسیقیایی باشد. در ابتدا هر نوازنده في البداهه یک دانگ صدا، از دامنه دانگهای صدای ممکن {Do , Re , Mi , Fa , Sol , Si , La} ساز موسیقی خود را می نوازد که در نهایت منجر به تولید یک هارمونی و همنوازی جدید خواهد شد، این هارمونی تازه به وسیله استانداردهای صوتی – زیبایی ارزیابی می شود. نوازندگان دانگهای صدای خوب را در حافظه خود نگه داری میکنند، و آنها را به جای بدترین هارمونی هایی که قبلا در حافظه شان ذخیره شده اند، برای استفاده در تمرین های بعدی قرار می دهند با تمرین های پی درپی دانگهای صدای بهتر در حافظه نوازندگان ذخیره می شوند، که این را می توانند به جای بدترین هارمونی هایی که قبلا در حافظه شان ذخیره شده اند، اختصاص دهند و به آنها یک شانس برای تولید یک هارمونی و همنوازی خوشایند و مطلوب را در تمرین های بعدیشان می دهد.
این را می توان در فرآیند بهینه سازی به این صورت معنی کرد: یک مجموعه از متغیرهای تصمیم گیری که توسط مقدارهایی تخصیص داده شده است، با تکرارهای پی در پی به دنبال یک جواب به اندازه کافی خوب هستیم، که توسط یک تابع هدف ارزیابی می شود. در ابتدا به هر متغیر تصمیم گیری، مقداری از دامنه شدنی اختصاص داده می شود، در نهایت یک بردار جواب جدید با همه ی متغیرهای تصمیم گیری ایجاد خواهد شد، که بردار جواب به وسیله تابع هدف ارزیابی می شود. متغیرهای تصمیم گیری ذخیره شده با مقادیر خوب، به جای بدترین بردارهای جواب که در حافظه ذخیره شده اند، قرار داده میشوند قبل از آن که در تکرارهای بعدی استفاده شوند.
تکرارهای پی در پی مقادیر خوبی برای هر متغير تصمیم گیری می دهند و در حافظه ذخیره خواهد شد، و به آنها یک فرصت برای ایجاد یک جواب بهتر در تمرین های بعدیشان را میدهد. جدول زیر ارتباط با وابستگی بین شرایط بهینه سازی و مفهوم های موسیقی را نشان میدهد. شكل زیر مقایسه بین فرآیند بداهه نوازی در موسیقی و فرآیند بهینه سازی را نشان می دهد.
هنگامی که یک نوازنده یک دانگ صدا از آلات موسیقیایی را بداهه نوازی می کند او سه گزینه دارد:
- هر دانگ صدا را از حافظه اش بداهه نوازی کند.
- یک دانگ صدا که در حافظه اش وجود دارد را اصلاح کند.
- هر دانگ صدا از دامنه دانگهای صدای ممکن را بداهه نوازی کند.
در بهینه سازی مقدار هر متغير تصمیم گیری، با توجه به یکی از گزینه های زیر اختصاص داده می شود:
- یک مقدار ذخیره شده در حافظه اش را اختصاص دهد.
- یک مقدار که در حافظه اش وجود دارد را اصلاح کند.
- یک مقدار از دامنه شدنی را اختصاص دهد.
این سه گزینه را می توان در سه عملگر زیر تحت قاعده و قانون درآورد:
- در نظر گرفتن حافظه
- تنظیم دانگ صدا
- در نظر گرفتن تصادفی
این عملگرها به وسیله دو پارامتر کنترل می شوند که عبارتند از:
- نرخ حافظه هارمونی در نظر گرفته شده (HMCR)
- نرخ تنظیم دانگهای صدا(PAR)
شکل 2 ساختار حافظه هارمونی را نشان میدهد که بخش اصلی فرایند بداهه نوازی است. آلات موسیقی را از پنج نوازنده در دسته موسیقی جاز به شرح زیر در نظر بگیرید: گیتارزن (سه تار)، ترومپت زن (شيپورزن)، درامر(طبل زن)، ساکسیفون، دو ويلون سل مجموعه ای از دانگهای صدای برتر در حافظه نوازندگان وجود دارد:
- گیتاریست: { Do, M , Sol }
- ترومپت زن: { La, Sa , Sol }
- درامر: { Re, Sol , Sa }
- ساکسیفون: { Fa, Do , La }
- دو ويلون سل: { Re, Sol , Mi }
فرض کنید در یک تمرین اگر گیتاریست به طور تصادفی و فی البداهه {Do} را از حافظه اش بنوازد و ترومپتزن في البداهه {Sol} از حافظه اش بنوازد، در امر {Re} را با {Fa} از حافظه اش تنظیم کند، ساکسیفون في البداهه {La از حافظه اش را بنوازد و دو ويلون سل {Si} را از دامنه موجود {Do , Re , Mi , Fa , Sol , Si} بنوازند. همه ی این دانگهای صدا با یکدیگر یک هارمونی تازه { Do, Sol , Fa , La , Si} را به وجود می آورند که به وسیله استانداردهای صوتی و زیبایی ارزیابی می شوند. اگر هارمونی تازه از بدترین هارمونی ذخیره شده در حافظه بهتر باشد، حافظه هارمونی به وسیله جایگزینی بدترین هارمونی با هارمونی جدید به روز می شود، این روند تا دست یافتن به یک هارمونی خوشایند تکرار خواهد شد. وضعیت شبیه بهینه سازی حقیقی است، پنج متغير تصمیم گیری در نظر بگیرید هر یک از مقادیر تجارب ذخیره شده در حافظه هارمونی به شرح زیر است:
- x1= {۱۰۰, ۲۰۳,۵۰۴}
- x2 = {۲۲۰,۴۰۰,۷۰۰}
- x3 = {۱۰۴, ۵۰,۶۰۰}
- x4 = {۱۰۰, ۲۰۰, ۳۰۰}
- x5 = {۷۰, ۲۵۰, ۳۰۰}
تابع بنچمارک تست الگوریتم هارمونی
توابع بنچمارک (Benchmark) زیادی برای سنجش عملکرد الگوریتمهای فراابتکاری ارائه شده اند که اسفیر (Sphere) به عنوان یک تابع پیوسته یکی از این توابع پرکاربرد میباشد. مقادیر متغیرهای این تابع در محدوده [-5.12 , 5.12] تعریف میگردند و مقدار پاسخ نیز برابر 0 می باشد که با اختیار نمودن تمامی متغیرهای آن بدست میآید. رابطه ریاضی این تابع به صورت زیر تعریف میگردد.
مساله فروشنده دوره گرد (TSP)
در این مساله یک فروشنده قصد دارد از تعدادی شهر عبور کند هدف این است که از تمام شهرها عبور کرده و همچنین کوتاهترین مسیر نیز انتخاب شود. همچنین هزینه رفتن مستقیم از شهره ها را نیز به عنوان ورودی ها مساله در اختیار داریم. مدل کلی این مساله به صورت زیر می باشد.
در این مدل، دسته محدودیت اول نشان می دهد که به هر گره j فقط یک یال وارد می شود. همچنین دسته دوم محدودیت دوم به این نکته اشاره دارد که از هر گره i فقط یک یال خارج می شود. محدودیت سوم باعث می گردد که الگوریتم جواب هایی را که در آن یک زیردور فاقد انبار تشکیل شده است، به عنوان جواب قابل قبول در نظر نگیرد. باید توجه نمود که محدودیت های اول و دوم سبب می شوند که به هر گره فقط یک یال وارد و نیز تنها یک یال خارج شود. دسته محدودیت چهارم نیز شرایط متغیر باینری Xij را بیان می نماید.
در این پروژه، توسط تابع بنچمارک عملکرد الگوریتم جستجوی هارمونی بررسی می شود همچنین به عنوان اشانتیون نیز کد متلب (MATLAB) مساله فروشنده دوره گرد توسط الگوریتم هارمونی در پکیج قرار داده شده است.
فایلهایی که بعد از خرید دانلود می کنید:
- کد متلب عملکرد جستجوی هارمونی
- گزارش ورد عملکرد جستجوی هارمونی و طریق کد نویسی
- ویدیوی آموزشی توضیح کدها و موارد مربوط به جستجوی هارمونی
- کد متلب و گزارش ورد مساله فروشنده دوره گرد توسط الگوریتم جستجوی هارمونی
نحوه تهیه: از طریق لینک زیر به درگاه بانک متصل شوید پرداخت آنلاین انجام می شود و سپس لینک دانلود نمایش داده می شود.