آموزش روش promethee
روش تصمیم گیری Promethee
تکنیک پرامتی (Promethee) که در بسیاری از ترجمه ها به نام پرومته معروف است و ماژول گایا در میان گسترده ترین روشهای استفاده شده در زمینه تصمیم گیری با معیارهای چند گانه است. متدولوژی پرامتی 1 (Promethee 1) که دسته بندی جزئی و همچنین پرامتی 2 (Promethee 2) که دسته بندی کامل انجام میدهد، نخستین بار در سال 1982 توسط پروفسور برانس توسعه داده شده و در همان سال های اولیه کاربرد فراوانی پیدا کرد. چند سال بعد پروفسور برانسبه کمک مارشال دو نسخه جدیدتر پرامتی یعنی پرامتی 3 (رتبه بندی مبتنی بر بازه ها) و پرامتی 4 (موارد پیوسته) را توسعه دادند. همچنین دو محقق مذکور در سال 1998 ماژول تصویری گایا را توسعه دادند. این ماژول نمایش گرافیکی جالبی را فراهم می کند که از پرامتی پشتیبانی می کند.
روش پرومته از سوي دانشگاهيان و محققين مورد اقبال قرار گرفته است و مقالات زيادي با بهره گيري از اين تكنيك نوشته شده است . اين روش براي ارزيابي و اولويت بندي گزينه هاي گسسته و انتخاب بهترين گزينه براساس چندين معيار (با مقياسهاي مختلف اندازه گيري) بكار مي رود. در استفاده از تكنيك پرومته، براي جبران ضعف يك معيار يا قوت معيار ديگر، محدوديت وجود دارد و لذا يك گزينه ايده ال بايد حداقل ها را از تمام معيارها كسب كند.
علاوه بر اين روش پرومته به راحتي قادر به بكارگيري معيارهايي با مقياس هاي مختلف اندازه گيري (بدون نياز به همسان سازي مقياس معيارها) مي باشد و متناسب با اطلاعات و مقياس معيار توابع شش گانه مجزايي را تعريف مي كند، لذا در تصميم گيري هاي چندمعياره كه معمولا معيارها داراي مقياس هاي مختلف اندازه گيري مي باشد يك نقطه قوت براي تصميم گير محسوب مي شود.
در فیلم زیر روش پرامتی به همراه معرفی و بررسی گامها توضیح داده شده است همچنین در مورد نرم افزار این روش مطالبی آورده شده. پیشنهاد می شود حتما این ویدیو را مشاهده کنید.
توابع ترجیح در پرامتی (Promethee)
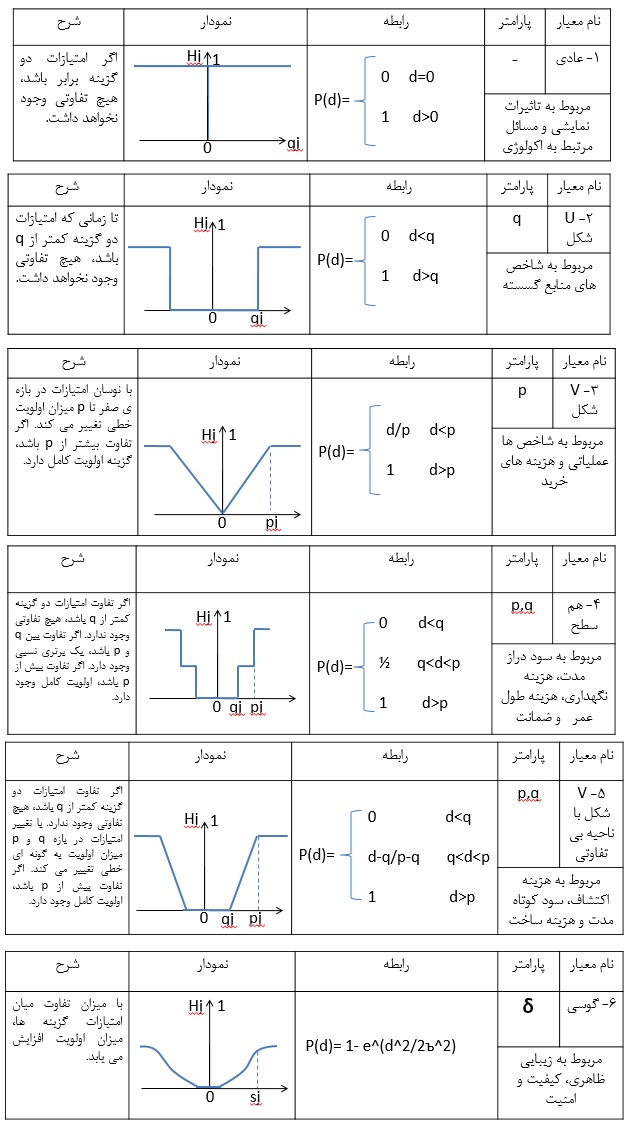
بطور کلی شش نوع تابع ترجیح پیشنهاد شده است که در جدول زیر آورده شده است تجربه نشان داده است که شش نوع تابع ارجحیت مذکور برای بیشتر مسائل واقعی جهان رضایت بخش است. با این حال هیچ اجباری به استفاده کردن از این نوع شش تابع ارجحیت وجود ندارد و تصمیم گیرنده می تواند تابع ارجحیت های دلخواه خود را برای ساختن معیار تصمیم یافته در نظر گیرد.
در توابع فوق پارامترهای q و p و s به ترتیب عبارتند از آستانه بی تفاوتی، آستانه برتری و آستانه مقدار میانی بین p و q. به عبارت بهتر q بزرگترین اختلافی است که تصمیم گیرنده می تواند در مقایسه دو گزینه نادیده بگیرد.
روش پرامتی 1 (Promethee 1)
در این روش هدف رتبه بندی جزیی گزینه ها می باشد. تعریف شاخص ها به صورت زیر است.
شاخص π(a,b) بیان می کند با چه درجه ای گزینه a با توجه به تمام گزینه ها بر گزینه b برتری دارد و π(b,a) بیان می کند که گزینه b با توجه به تمام گزینه ها چقدر بر گزینه a برتری دارد. در بیشتر موارد هر دو شاخص فوق مثبت هستند و بدین معنی است که گزینه a در بعضی معیارها بر گزینه b برتری دارد و گزینه b هم در برخی معیارها بر a برتری دارد. ممکن است دو گزینه در بعضی معیارها با هم یکسان باشند.
- اگر π(a,b)=0 باشد تمامی مقادیر pj(a,b) برابر صفر است و این بدان معناست که a هیچ برتری بر b ندارد.
- اگر π(a,b)=1 باشد تمامی مقادیر pj(a,b) برابر یک است و این بدان معناست که a کاملا بر b ارجحیت دارد.
روش پرامتی 2 (Promethee 2)
براي ارزيابي و اولويت بندي گزينه هاي گسسته و انتخاب بهترين گزينه روش پرومتهII بكار مي رود . اين روش در جايي كه بايد گزينه هاي بي شماري بر اساس چند معيار كمي و كيفي و اغلب متناقض ارزيابي شود، سازگار و كارا مي باشد. در
اين روش ابتدا هر معيار تصميم، براساس تابع مجزا و بدون ارتباط با ساير معيارها مورد توجه قرار ميگيرد. پرومته براي تفاوت هاي دوبه دوي گزينه ها براساس هر معيار، آستانه هاي معنيداري و غيرمعني داري تفاوت ها را تعريف كرده و بدين ترتيب تفاوت هاي اندك (كمتر از q ) كه احتمال دارد ناشي از تصادف باشد را حذف مي كند، از طرف ديگر در مورد تفاوت هاي بزرگ، تفاوت بيشتر از مقدار p را برابر p در نظر مي گيرد (p=p>d)، به عبارت ديگر تفاوت بيشتر از مقدار آستانه (p ) مزيت و نمره اضافي تر براي يك گزينه در يك معيار محسوب نمي شود.
هنگامی که روش پرامتی 1 در در رتبه بندی بعضی گزینه ها ناتوان باشد از پرامتی 2 استفاده می شود. جریان ترجیحات به منظور منظم کردن نتایج مقایسات زوجی و رتبه بندی گزینه ها است سه نوع مختلف جریان ترجیحات وجود دارد:
- +Phi جریان مثبت است که از رابطه زیر بدست می آید و میزان ارجحیت a نسبت به n-1 گزینه دیگر را بررسی می کند این در واقع میزان قدرت گزینه a می باشد هر چه قدرت +Phi بیشتر باشد گزینه a بهتر است.
- -Phi جریان منفی است که از رابطه زیر بدست می آید و میزان ارجحیت n-1 گزینه دیگر را نسبت به گزینه a بررسی می کند این در واقع میزان ضعف گزینه a می باشد هر چه قدرت -Phi کمتر باشد گزینه a بهتر است.
- Phi جریان خالص است که از رابطه زیر بدست می آید در واقع بیانگر مقادیر جریان مثبت و منفی بصورت همزمان می باشد هر چه قدرت Phi بیشتر باشد گزینه a بهتر است.
مثال روش Promethee
در این مثال هدف رتبه بندی سه گزینه A1 و A2 و A3 بر اساس 4 معیار C1 تا C4 می باشد که معیارهای C1 از نوع منفی و سه معیار دیگر جنبه مثبت دارند. همچنین از ورودی های این مدل باید وزن معیارها را نیز در اختیار داشته باشیم این اوزان را می توان از روشهایی نظیر AHP و یا آنتروپی محاسبه کرد. ماتریس تصمیم مقال به همراه وزن معیارها و دیگر اطلاعات در جدول زیر آورده شده است.
| معیارها | گزینه ها |
||||
| (C4) | (C3) | (C2) | (C1) | ||
| 0.267 | 0.336 | 0.092 | 0.305 | ||
| مثبت | مثبت | مثبت | منفی | نوع شاخص | |
| ۴ | ۵ | ۳ | ۳ | نوع تابع | |
| ۱ | ۳ | – | – | q | |
| ۳ | ۱۰ | ۵ | ۵ | P | |
| ۴ | ۱۳ | ۸ | ۵ | A1 | |
| ۲ | ۹ | ۱۰ | ۴ | A2 | |
| ۳ | ۶ | ۱۲ | ۸ | A3 | |
در گام اول باید تفاوت گزینه ها را نسبت به معیارهایی که در آن ارجح هستند را بدست آورد که در جدول زیر آورده شده است.
| C4 | C3 | C2 | C1 | ||
| ۲ | ۴ | ۰ | ۰ | A2 | ميزان تفاوت A1 با گزينه هاي ديگر |
| ۱ | ۷ | ۰ | ۳ | A3 | |
| ۰ | ۰ | ۲ | ۱ | A1 | ميزان تفاوت A2 با گزينه هاي ديگر |
| ۰ | ۳ | ۰ | ۴ | A3 | |
| ۰ | ۰ | ۴ | ۰ | A1 | ميزان تفاوت A3 با گزينه هاي ديگر |
| ۱ | ۰ | ۲ | ۰ | A2 |
در گام دوم باید مقادیر (Pj(a,b را با توجه به توابع داده شده محاسبه کرد. که در جدول زیر آورده شده است.
| C4 | C3 | C2 | C1 | P1 | ارجحیت A1 با گزينه هاي ديگر |
| ۱/۲ | ۱/۷ | ۰ | ۰ | A2 | |
| ۰ | ۴/۷ | ۰ | ۳/۵ | A3 | |
| C4 | C3 | C2 | C1 | P2 | ارجحیت A2 با گزينه هاي ديگر |
| ۰ | ۰ | ۲/۵ | ۱/۵ | A1 | |
| ۰ | ۰ | ۰ | ۴/۵ | A3 | |
| C4 | C3 | C2 | C1 | P3 | ارجحیت A3 با گزينه هاي ديگر |
| ۰ | ۰ | ۴/۵ | ۰ | A1 | |
| ۰ | ۰ | ۲/۵ | ۰ | A2 |
در گام سوم شاخص های ارجحیت ادغامی را محاسبه می کنیم.
| π(۳,۱)= 0.0736 | π(۲,۱)= 0.0975 | π(۱,۲)= 0.1815 |
| π(۳,۲)= 0.368 | π(۲,۳)= 0.244 | π(۱,۳)= 0.375 |
| π(۳,x)= 0.1104∑ | π(۲,x)=0.3418∑ | π(۱,x)= 0.5565∑ |
| π(x,3)= 0.619∑ | π(x,2)= 0.2183∑ | π(x,1)=0.1714∑ |
در گام چهارم بدست آوردن جريانهاي مثبت و منفي، و بعد جريان خالص جهت رتبه بندي.
| Phi | -Phi | +Phi | |
| ۰٫۱۹۲۳ | ۰٫۰۸۵۷ | ۰٫۲۷۸۳ | A1 |
| ۰٫۰۶۱۷ | ۰٫۱۰۹۲ | ۰٫۱۷۰۹ | A2 |
| -۰٫۲۵۴۳ | ۰٫۳۰۹۵ | ۰٫۰۵۵۲ | A3 |
سپس در گام آخر بر اساس جریان خالص گزینه ها را رتبه بندی میکنیم که گزینه A1 رتبه اول و گزینه A2 رتبه دوم و گزینه A3 رتبه سوم را کسب کرده است.
تاریخچه PROMETHEE
در تحقیقی که برای انتخاب بهترین توزیع آماری با استفاده از روش PROMETHEE و GAIA انجام شد ، نتایج حاصل نشان داد که روش PROMETHEE روش قابل قبولی برای انتخاب بهترین توزیع آماری می باشد و به همین دلیل به استفاده از این روش توصیه شد (نمری و ایشیزاکا، 2011 ). در پژوهش دیگری به پیاده سازی روش PROMETHEE با تصمیم گیری چند معیاره پرداخته شد. در این تحقیق ثابت شد که روش PROMETHEE یک ابزار موفق برای ارزیابی رقابت لجستیکی کشورهای شبه جزیره بالکان است (تومیک و همکاران، 2011). در مطالعه ای که با ترکیبی از رویکرد AHP و PROMETHEE برای انتخاب مناسبترین سیاست برای برانگیختن ناوگان خودرو پاک استفاده شد، محققین پی بردند که ترکیبی از دو روش، محقق را قادر می سازد که ارزیابی دقیقی از شناسایی سناریوها که در آن نقاط ضعیف و قوی شناسایی و رتبه بندی شده انجام شود (تورکسین و همکاران، 2011). انتخاب مفهوم پایدار یک مشکل حیاتی برای سازمان های تولیدی معاصر است، زیرا که فرایند انتخاب شامل معیارهای چندگانه است. در تحقیقی با استفاده از روش PROMETHEE برای انتخاب بهترین مفهوم پایدار با توجه به معیارهای اجتماعی، اقتصادی، و محیط زیستی انجام شد (وی نود وگیروبا، 2012).
از طریق لینک زیر می توانید فیلم آموزش روش promethee را تهیه کنید:
چنانچه نیازمند مشاوره و یا انجام پروژه خود با این روشها هستید با ما تماس بگیرید| ۰۹۳۳۸۸۵۹۱۸۱

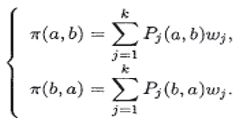
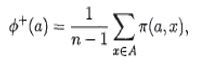

سلام
میشه توضیح بدید پرامتی 2 و 3 چه تفاوتی دارند با هم؟
بنده باید در مورد پرومته 3 توضیحات بدم در دانشگاه
روش پرامتی 3 بر اساس مقداره فاصله ای برای گزینه ها رتبه بندی را انجام می دهد.
ممنون از مطالبتون.