پروژه مسیریابی وسیله نقلیه (VRP) در گمز
|
فهرست مطالب 1- مقدمه |
مقدمه
یکی از مهمترین مسائل مدیریت زنجیرهی تأمین، مسئلهی مسیریابی وسایل نقلیه می باشد. اهمیت این موضوع به این دلیل است که اختصاص دادن مطلوب وسایل نقلیه به مسیرهای گوناگون، تأثیر بسیاری بر کاهش هزینهها خواهد داشت. که میتواند یکی از شناخته شده ترین مسائل در حوزه بهینه سازی و یکی از مفاهیم آشنا در تحقیق در عملیات محسوب می شود . در دو دهه اخیر تلاشها و پیشرفتهای زیادی در این حوزه صورت گرفته است. مسأله مسیریابی وسایل نقلیه به این معنا است که ناوگانی تشکیل شده از چندین وسیله نقلیه از یک یا چند انبار به خدمت رسانی در مناطق مختلف جغرافیایی بپزدازند و این عمل را بگونه ای انجام دهند که هزینه ها به پایین ترین حد برسد.
در این مطلب به مساله مسیریابی وسایل نقلیه (VRP) به همراه محدودیت پنجره زمانی پرداخته می شود.در واقع مدل یک مقاله ISI در محیط نرم افزار گمز (Gams) پیاده سازی می شود که در انتهای این پست جهت دانلود قرار داده شده است.
مساله مسیریابی وسایل نقلیه با محدودیت پنجره های زمانی
این مدل بسط مهمی از مسئله مسیریابی وسایل نقلیه می باشدو در واقع مسئله پایه مدیریت توزیع است که می تواند مدلی برای تمام مسائل دنیای واقعی با طراحی مسیرهایی با حداقل هزینه، دارا بودن یک دپوی مرکزی برای تمام وسایل نقلیه سرویس دهنده با تقاضاهای مشخص باشد. ظرفیت وسایل نقلیه در طول مسیر خدمت رسانی قابل افزایش نمی باشد. مسئله مسیریابی وسایل نقلیه با محدودیت پنجره های زمانی، دارای کاربردهای فراوانی در دنیای واقعی است. بعضی از کاربردهای این مدل عبارتند از:
سیستم های حمل و نقل و لجستیک (حمل و نقل زمینی، زیر زمینی، هوایی، جاده ای، دریایی، حمل و نقل ریلی، مونوریلی)، حمل ونقل مواد خطرناک، حمل مواد فساد پذیر و زباله های بیمارستانی، توزیع فرآورده های نفت و گاز، توزیع محموله های کشتیرانی، توزیع محموله های بانکی، جمع آوری زباله های شهری، مسیریابی سرویس های مدارس، و زنجیره تامین، سیستم های تصمیم گیر پشتیبان، توزیع محموله های پستی، توزیع سفارشات رستوران ها، تقسیم سوخت بین جایگاه های سوخت و …
توضیحات مقاله
مساله مسیریابی وسایل حمل و نقل با پنجره زمانی (VRPTW) مساله تعمیم یافته ای از مساله مسیریابی وسایل حمل و نقل با محدودیت ظرفیت (CVRP) است که در آن سرویس به هر مشتری باید در یک بازه زمانی معین (این بازه زمانی به پنجره زمانی معروف است) صورت گیرد.
← عنوان فارسی مقاله: مساله مسیریابی وسیله نقلیه با محدودیت پنجره زمانی
paper title: A hybrid algorithm for vehicle routing problem with time windows→
انواع VRP
یافتن مسیرهاي نقلیه کارا یک مساله لجستیک است که در چهل سال اخیر مطالعه شده است نوعاً هدف یک مساله مسیریابی وسایل نقلیه (VRP ) پیدا کردن مجموعهاي از مسیرها براي چندین وسیله نقلیه از یک انبار به تعدادي مشتري و برگشتن به انبار، بدون این که محدودیت ظرفیت هر وسیله نقلیه نقض شود، با مینیمم هزینه است. چون ترکیب مشتري ها به انتخاب مسیرهاي حمل و نقل محدود نیست، VRP به عنوان یک مساله بهینهسازي ترکیباتی مورد توجه است به طوري که تعداد جواب هاي شدنی براي مساله به طور نمایی با رشد تعداد مشتري ها زیاد می شود.
به هر مسأله که به دنبال تولید یک تور یا مجموعه ای از تورها بر روی یک شبکه یا زیر شبکه با هدف بهینه ساختن یک یا چند تابع هدف باشد، مسئله مسیریابی گفته می شود. تمامی این مسائل یک حالت خاص از مسئله فروشنده دوره گرد به شمار می آیند. هدف از این مسأله، پیدا کردن کوتاهترین مسیری است که از مجموعه ای از شهرها (گره ها عبور کرده، به گونه ای که هر شهر فقط يكبار ملاقات شود و سپس به شهر اولیه که حرکت را از آن شروع کرده است، بر گردد. مسئله VRP نقش مهمی در زنجیره تأمین ایفا می کند، برای مثال در اولین مرحله از انتقال (مانند جمع آوری محصولات کشاورزی) و یا توزیع به مشتری در مرحله ی نهایی سیستم توزیع در مسئله مسیریابی وسایل نقلیه عموما بر اساس مفاهیم تئوری گراف مدل می شود.
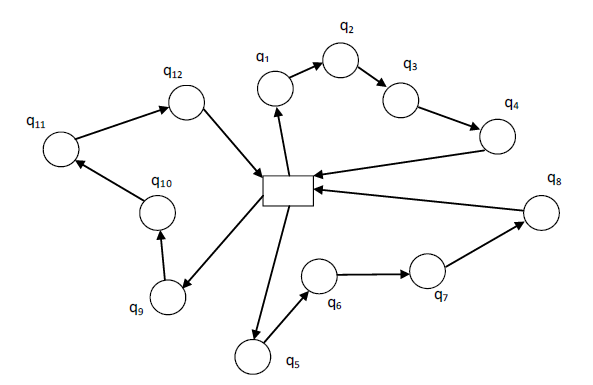
در این حالت گره های گراف بیانگر مشتریان و یال های آن بیانگر راههای موجود بین مشتریان است. هزینه به صورت زمان یا مسافت، متناسب با هر یال گراف تعریف می شود. بسته به | اینکه مسیرها یک طرفه یا دوطرفه باشند یا هزینه سفر رفت و برگشت بین دو گره یکسان یا غیر یکسان باشد، گراف های جهت دار یا غیر جهت دار تعریف می شوند. به این ترتیب اگر بین هر دو مشتری امکان سفر رفت و برگشت با هزینه یکسان وجود داشته باشد، مسأله با تعریف گراف سادهی غیر جهت دار مدل می شود.
شکل زیر نمایی از مسئله VRP را در حالت کلاسیک نشان می دهد. اجزای مسئله مسیریابی وسایل نقلیه را در حالت معمول می توان به مجموعهی مشتریان، مجموعه ی وسایل نقلیه (خودروها، ناوگان حمل و نقل) و شبکهی جاده ای (مسیرها) تقسیم بندی کرد. هر یک از این اجزا خصوصیاتی دارند که به عنوان فرضیات مسأله و پارامترهای ورودی مد نظر قرار می گیرند.
معمول ترین و مهمترین هدف مسئله مسیریابی، حداقل کردن کل هزینه سیستم است. گاهی به جای حداقل کردن هزینه از حداقل کردن کل مسافت طی شده توسط وسایل نقلیه یا مجموع زمان استفاده از آنها، در تابع هدف استفاده می شود.
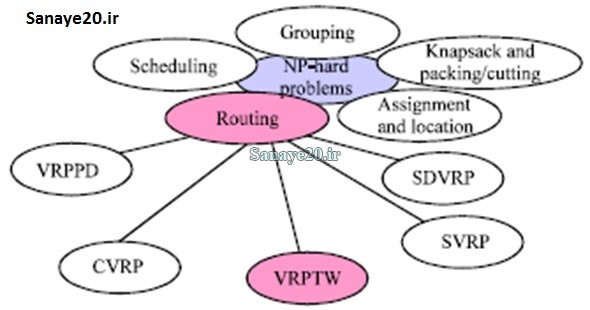
در دنیای واقعی در مسائل VRP قیدهایی نظیر قیدهای زیر ظاهر می شوند که رعایت آنها به شدت در انتخاب راه حل تاثیر گذار است. اگرچه الگوریتم های حل این مسئله به سمتی می روند که قابلیت انعطاف با قیدهای مختلف را داشته باشند. با توجه به نوع قید نام های گوناگونی به خود می گیرد که در زیر آورده می شود:
- هر وسیله حجم محدودی دارد (CVRP)
- هر مشتری باید در محدوده ی زمانی مشخصی سرویس دهی شود (VRPTW)
- فروشنده از انبارهای متعددی برای سرویس دهی به مشتریان استفاده می کند (MDVRP)
- مشتری ها ممکن است مقداری از کالا را به انبار برگردانند (VRPPD)
- مشتری ها ممکن است توسط چند وسیله توزیع سرویس دهی شوند (SDVRP)
- بعضی مقادیر مانند تعداد مشتری ها، درخواست هایشان، محدودیت زمانی سرویس دهی یا زمان سفر ممکن است به صورت تصادفی انتخاب شود (SVRP)
- تحویل کالا ممکن است فقط روزهای مشخصی صورت پذیرد (PVRP)
مدل مسیریابی وسیله نقلیه
حمل و نقل در دنیای صنعتی امروز نقش مهمی در توسعه اقتصادی کشورها به وسیله فراهم آوردن امکان مصرف محصولات در محل های بسیار دور از محل تولید، دارد. ارائه محصول نهایی به یک مشتری مستلزم انتقال مواد اولیه از تأمین کنندگان به تولید کنندگان، انتقال محصولات نیمه تمام بین کارخانه ها، و سرانجام رساندن محصول نهایی به مشتریان و بازارهای مقصد است. به دلیل تعدد فعالیت های حمل و نقل، هزینه های حمل و نقل درصد بالایی از هزینه های لجستیک (بین 30 تا 60 درصد) را در بر می گیرند. بنابراین حمل و نقل کارآمد در تمام طول زنجیره تأمین از اهمیت بالایی برخوردار است. با استفاده از سیستم های حمل و نقل کارآمد می توان بازارهای فعال کنونی را گسترش داد و نیز بازارهای جدید ایجاد کرد، محصولات فاسد شدنی را در حداقل زمان به مصرف کنندگان در سراسر دنیا رساند، و از مزیت های رقابتی کشورهای در حال توسعه برای تولید ارزان تر محصولات استفاده کرد. تصمیمات حمل و نقل، که در سطح تاکتیکی تصمیمات لجستیک هستند، برخلاف تصمیمات مکان یابی با سهولت بیشتری قابل بهینه سازی مجدد نسبت به شرایط و ساختار تغییر یافته زنجیره تأمین هستند. بنابراین این تصمیمات نسبت به شرایط نوسانی محیط های صنعتی کمتر آسیب پذیر هستند.
مسئله مسیریابی وسیله نقلیه، که اولین بار توسط دانتزیک و رامزر معرفی شد، یکی از مهمترین مسائل بهینه سازی از دو دیدگاه تحقیقاتی و عملیاتی است که مربوط به مبحث طراحی سیستم های صنعتی می باشد. این مسئله که حالت ترکیبی از دو مسئله فروشنده دوره گرد نامحدود در نظر گرفتن ظرفیت وسیله نقلیه) و بسته بندی صندوق ها (صفر در نظر گرفتن هزینه حمل و نقل بر روی بال ها) است، سعی در طراحی بهینه مجموعه ای از مسیرها برای ناوگان حمل و نقل به تعوی دارد که به تعداد معینی مشتری خدمت رسانی شود و دارای محدودیت های جانبی مختلفی است که از آن جمله می توان به محدودیت های ظرفیت وسایل نقلیه، پنجره زمانی، چند تسهیلی، بارگیری و تحویل اشاره کرد.
معمولي ترين و در عين حال مهمترين هدف مسأله VRP حداقل كردن كل هزينه سيستم است. گاهي اوقات به جاي حداقل كردن هزينه، از معادل هاي آن يعني كل مسافت طي شده توسط خودروها يا مجموع زمان استفاده از آنها در تابع هدف استفاده مي شود.
.1حداقل كردن هزينه (زمان – سفر) كل سيستم.
.2استفاده از حداقل تعداد خودروهاي ممكن براي سرويس دهي به مشتريان.
.3ماكزيمم كردن تعداد مشترياني كه توسط خودروها به آنها سرويس داده مي شود.
.4بالانس سيستم براي امكان سرويس دهي به مشتريان در بازه هاي زماني تعيين شده.
.5حداقل كردن زيان هاي ناشي از عدم برآورده شدن برخي خواسته هاي مشتريان.
.6حداقل كردن زيان هاي ناشي از عدم استفاده از كل ظرفيت خودروها.
در بسیاری از سیستم های خدماتی نظیر حمل و نقل مسافران و سرویس های خدماتی تعمیرات و نگهداری، مشتریان می بایستی توسط مجموعهای از وسایل نقلیه سرویس دهی شوند. این ناوگان حمل و نقل در یک مکان استقرار یافته اند. هدف پیدا کردن مجموعه ای از مسیرها می باشد به گونه ای که مجموعه ای از محدودیت ها را ارضا کند و کل مسیر طی شده توسط وسایل نقلیه و سایر هزینه ها کمینه شود. این مساله، مساله مسیریابی وسیله نقلیه نام گذاری شده و دربسیاری از مجلات معتبر علمی به صورت گسترده مورد تجزیه و تحلیل قرار گرفته است. هدف از مساله VRP در شرایط کلاسیک، کمینه سازی کل مسافت طی شده توسط وسایل نقلیه، کاهش حجم ناوگان، کمینه سازی جریمه های دیرکرد یا زودکرد سرویس دهی و در نهایت افزایش رضایت مشتریان است. مساله مسیریابی وسایل نقلیه در واقع توسعه ای از مسئله معروف فروشنده دوره گرد بوده است. از همان سالهای اولیه معرفی این مسئله توسعه های زیادی بر روی این موضوع شروع به شکل گرفتن گرفت. این مسئله با توجه به اهمیت بالایی که به بحث زمان درحل مسایل می دهد در عمل از کاربرد بیشتری برخوردار بوده و لذا توجه بیشتری را در محافل علمی به خود اختصاص داده است.
در حالت خاص می توان جواب حاصل از مساله مسیریابی را به صورت زیر بیان نمود:
تعیین مجموعه ای از مسیرها که هر کدام توسط یک وسیله نقلیه مورد استفاده قرار میگیرند (البته وسایل نقلیه از مراکز توزیعی که اعزام میشوند در نهایت به همان مرکز توزیع نیز بر می گردند)، به نحوی کوه نیاز مشتری برآورده شود و تمام محدودیت های عملیاتی نیز ارضا شده و نتیجه به حداقل شدن هزینه کل منجر شود.
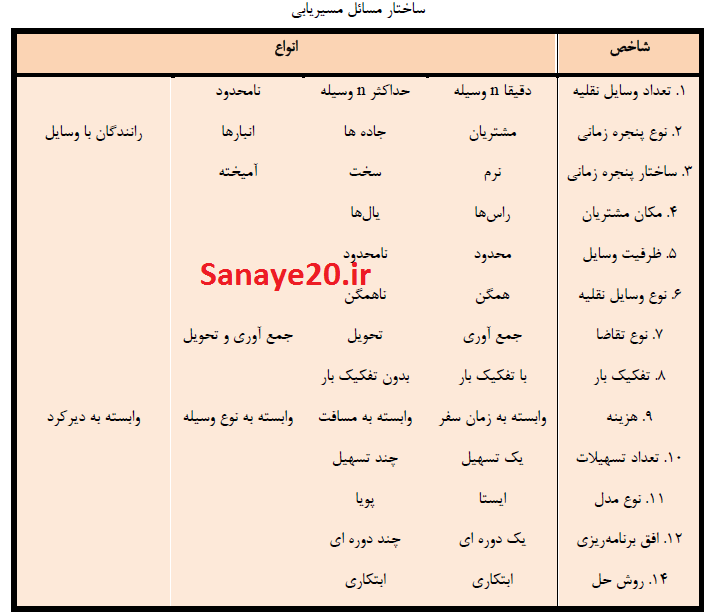
در جدول زیر دسته بندي ارائه شده توسط بوراک و همکاران در سال 2009 آورده شده است:
مدلی که در این مقاله بررسی می شود در زیر آورده شده است. هدف مدل پیشنهادی کمینه سازی طول کل سفر است. همچنین علاوه بر محدودیت های سنتی، مدل شامل محدودیت های مرتبط با پنجره های زمانی می باشد. با توجه به علائم، پارامترها و متغیرهای تعریف شده، مدل ریاضی پیشنهادی متشکل از یک تابع هدف و چندین دسته محدودیت می باشد که پس از معرفی مدل ریاضی توضیحات بیشتری در مورد تابع هدف و محدودیت ها ارایه خواهد
محدودیت های مدل
- محدودیت a، محدودیت حداکثر تعداد مسیرها را نشان می دهد (حداکثر K مسیر از انبار به خارج می شود).
- محدودیت b، محدودیت سفررا نشان می دهد( هر مسیر شروع و پایانش به انبار است).
- محدودیت های c-d، محدودیت های سرویس دهی را نشان می دهند( هر مشتری تنها یکبار توسط وسیله نقلیه ملاقات می شود).
- محدودیت e، محدودیت ظرفیت است.
- محدودیت f، محدودیت ماکزیمم زمان سفر است.
- محدودیت های g-h-i، محدودیت های پنجره زمانی هستند.
انواع روشهای حل
مسئله مسيريابي وسيله نقليه، اولين بار توسط دانزيگ و رامسر در سال 1959 میالدی معرفي شد. اين مسئله بر روي تحويل کالا به مشتريان با تقاضاي مشخص تمرکز ميکند؛ به صورتی که شروع و پايان مسیر در انبار است. مین در سال 1989 میلادی محدوديت جديدي را براي مسئله مسيريابي وسيله نقليه تعريف نمود. او مسئله حمل و نقل کتاب بين کتابخانه ها را به شکل فرموله شده درآورد که به مسئله مسيريابي با تحويل و دريافت همزمان معروف شد . همچنین او از رويکرد دو مرحله اي براي حل اين مسئله استفاده کرد. در اولين مرحله، مشتري ها با اين شرط که مجموع تقاضاهاي تحويل يا مجموع دريافت ها در داخل آن مسير کمتر از ظرفيت وسيله نقليه باشد، در گروه هايي خوشه بندي شدند. در دومين مرحله، مسئله فروشنده دوره گرد به طور کامل حل شد؛ به صورتی که اگر مسير فروشنده دوره گرد محدوديت ظرفيت وسيله نقليه را نیز نقض مي کرد، مسئله دوباره حل مي شد.
دتلوف در سال 2001 میلادی کاربردهاي مسئله مسيريابي وسيله نقليه دريافت و تحويل همزمان کاال را برای اولين بار در مسائل لجستيک معکوس برجسته کرد و از روش ابتکاري ارزانترين الحاقي براي حل مسئله استفاده نمود . مونتان و گالوو در سال 2002 میلادی، سه نوع متفاوت از مسئله مسيريابي وسيله نقليه دريافت و تحويل همزمان کالا را تعريف کردند. آنها مسئله هاي مزبور را با استفاده از الگوريتم هاي ابتکاري چرخه اي، حداقل شعاع پوشش درختي و الگوريتم ابتکاري ارزان ترين الحاقي حل کردند. عملگرهاي تعويض گره ها به منظور غلبه بر مسيرهاي امکان ناپذير و بهبود کيفيت حل مسئله مورد استفاده قرار گرفتند . آنجليا و مانسيني در سال 2002 ، محدوديت زماني را براي مسئله مسيريابي وسيله نقليه دريافت و تحويل همزمان کالا معرفي نمودند. تحقيقات آنها، اولين و تنها تحقيق انجام شده به منظور استفاده از يک الگوريتم دقيق براي حل نسخه اصلي مسئله است. آنها الگوريتم شاخه و ارزش را به صورت مجموعه ي فرموله شده توسعه دادند. زاچاراديس و همکاران در سال 2009 میلادی، يک چارچوب ترکيبي را بر اساس دو الگوريتم ابتکاري شناخته شده جستجوي ممنوعه و جستجوي محلي پيشنهاد دادند. اين روش با هدف دستيابي به يک تعادل رضايت بخش بين شدت و تنوع جستجو ارائه شده است. با اين منطق، اين روش با شدت بخشيدن در مناطق به صورت اميدوارکننده تری به جستجوي فضاي وسيعي از حل ها مي پردازد. بولنت ساتاي در سال 2010 میلادی، يک الگوريتم کلوني مورچه را توسعه داد که مجهز به يک تابع با ديد صرفه جويي و روش بروزرساني فرومون بود. نتايج ارائه شده نشان از قابليت الگوريتم پيشنهادي در یافتن فرومون کوتاهترين فاصله دارد. زاچاراديس در سال 2011 میلادی، يک الگوريتم فراابتکاري براي مسئله مسيريابي وسيله نقليه دريافت و تحويل همزمان کالا را ارائه داد که در آن، با استفاده از يک روش جستجوي محلي کارآمد به اکتشاف همسايگي جواب مي پردازد. او همچنين نتايج بدست آمده قبلي خود را در سال 2009 میلادی بهبود بخشيد.
ابتدا قبل از اینکه روش حل مشخص شود باید نوع مساله VRP نیز مشخص شود.
بر اساس مقاله ای از (کوردون(۲۰۰۱) چهار تابع هدف معمول این مسأله عبارتند از:
- کمینه کردن فاصله (زمان) كل سیستم
- استفاده از حداقل تعداد وسايل نقليهی ممکن برای سرویس دهی به مشتریان
- حداقل کردن مجموع زمان های تکمیل
- کمینه کردن مجموع طول مسیر
در حالت کلی اولین تابع هدف تعریف شده توسط کوردون می تواند به شکل زیر نیز مطرح شود:
کمینه کردن هزینه های مربوط به ناوگان و سرویس دهی شامل: هزینه کل مسافت طی شده توسط وسايل نقليه، هزینه ثابت و متغیر ناوگان همانند اجاره، حقوق و دستمزد، استهلاک و غيره و سایر هزینه های مرتبط با امور حمل و نقل. در عین حال در کاربردهای مختلف، علاوه بر اهداف ذکر شده، اهداف دیگری نیز می توان برای مسأله در نظر گرفت:
- ماکزیمم کردن تعداد مشتریانی که توسط خودروها به آنها سرویس داده می شود
- بالانس سیستم برای امکان سرویس دهی به مشتریان در بازه های زمانی تعیین شده (از جهت زمان سفر و حجم بار وسیله نقلیه)
- حداقل کردن زیان های ناشی از عدم برآورده شدن برخی از تقاضاهای مشتریان حداقل کردن زیان های ناشی از اضافه کاری راننده و استفاده بیش از حد از وسایل نقلیه
- حداقل کردن زیان های ناشی از عدم استفاده از کل ظرفیت وسایل نقلیه
- حداقل کردن زمان و تعداد مسافرت هر وسیله حداقل کردن زمان انتظار مسافرین و خسارت دیرکرد یا زودگرد ارائه ی خدمت به مشتریان.
ضمنا تابع هدف می تواند ترکیب وزنی از همه اهداف مذکور باشد.
مساله VRP وانواع مختلف آن جز مسایل NP-Hard محسوب می شوند که از نظر حل با بزرگ شدن ابعاد مساله با مشکلات جدی مواجه می شوند. گاهی اوقات حتی پیدا کردن یک جواب موجه برای مساله هم امکان پذیر نیست. لذا مطالعه روی روشهای حل مساله و ارائه الگوریتم هایی که امکان حل مسایل با ابعاد بزرگتر در دنیای واقعی را فراهم آورند و یا جواب های الگوریتم های موجود را بهبود دهند، از اهمیت بسزایی برخوردار است. روشهای حل مساله VRP را می توان در سه دسته عمده طبقه بندی کرد:
- الگوریتم های حل دقیق
- الگوریتم های هیوریستیک (ابتکاری)
- الگوریتم های متاهيوريستیک (فراابتکاری)
در ادامه این بخش به معرفی سه دسته الگوریتم های فوق خواهیم پرداخت.
الگوریتم های حل دقیق
مهمترین الگوریتم های پایه برای حل مسایل برنامه ریزی صحیح الگوریتم شاخه وحد (B&B) است که از آن در حل انواع مساله VRP استفاده فراوانی شده است. مشکل اصلی در بکارگیری از روش (B&B) در حل مساله VRP، افزایش ابعاد درخت محاسبات الگوریتم و در نتیجه افزایش زمان حل با بزرگ شدن ابعاد مساله است داشتن یک کران پایین (در مسایل مینیمم سازی) با کیفیت مطلوب (نزدیک به جواب بهینه) کمک زیادی به کاهش حجم محاسبات و زمان حال در الگوریتم (B&B) می کند. به منظور پسافتن و بهبود کران های پایین روی مساله VRP، از آزادسازی های ترکیباتی استفاده شده است. این آزادسازیها عبارتند از:
- Assignment Problem(AP)
- Degree constrained shortest spanning Tee(SST)
- State space Relaxations
- Lagrangian relaxation
الگوریتم های شاخه و برش (B&C) دسته دیگری از الگوریتم های حل دقیق مساله VRP هستند که علی رغم موفقیتشان در پیدا کردن جواب بهینه در مساله فروشنده دوره گرد (ISP)، در مساله VRP چندان مورد توجه قرار نگرفته اند.
الگوریتم های مبتنی بر Set-covering دسته سوم الگوریتم های حل دقیق برای VRP را تشکیل می دهند که برای مدلهایی از مساله VRP که بر اساس مسایل Set-covering شکل گرفته اند مطرح شده و توسعه یافته اند.
الگوریتم های هیوریستیک برای VRP
الگوریتم های هیوریستیک کلاسیک مساله VRP را می توان در سه دسته تقسیم بندی و توضیح داد. در دسته اول که به الگوریتم های سازنده مرسوم هستند الگوریتم به دنبال پیدا کردن یک جواب موجه برای مساله با نیم نگاهی به تابع هدف است ولی به دنبال بهبود جواب موجه نمی گردد. الگوریتم های دو فاز 4 دسته دیگری از هیوریستیکهای VRP هستند که در آنها در یک فاز جواب های موجه مساله دسته بندی و در فاز دیگر جواب نهایی انتخاب می شود و بالاخره دسته سوم الگوریتم های بهبود هستند که به بهبود یک جواب شدنی با تغییر توالی گره ها می پردازند.
الگوریتم های متاهيوريستیک برای VRP
در سالهای اخیر توجه زیادی به استفاده از الگوریتمهای متاهيوريستیک در حل مساله VRP شده است که دلیل آن به کیفیت جواب این الگوریتم ها و زمان کم حل آنها بر می گردد. 6 دسته الگوریتم متا هیوریستیک که برای حل مساله VRP استفاده شده اند عبارتند از:
- Simulated Annealing(SA)
- Deterministic Annealing(DA)
- Tabu Search(TS)
- Genetic Algorithm(GA)
- Ant Systems(AS)
- Neural Network(NN)
سه نوع الگوریتم اول از یک جواب اولیه x1 شروع کرده و در مرحله tام جواب xt+1 را در همسایگی جواب xt تولید می کند. این کار تا رویدادن شرط توقف ادامه می یابد. الگوریتم GA در هر مرحله جمعیتی از جواب های را آزمایش می کند تا به بهترین جواب دست یابد. در الگوریتم AS در هر مرحله جوابی بر اساس اطلاعات کسب شده در مراحل قبلی تولید می شود و سرانجام NN یک مکانیزم یادگیرنده است که با تطبیق یکسری وزن ها به جواب قابل قبول می رسد.
دوستان عزیز مدل ریاضی که در متن بالا توضیح داده شد در نرم افزار گمز حل شده است که از طریق لینک زیر می توانید آن را خریداری و دانلود نمایید. در فایل خریداری شده توضیحات این مدل، مقاله ISI و فایل گمز (Gams) پیاده سازی شده آورده شده است.
فایلهای دانلود: مقاله isi، کد گمز و توضیحات در قالب WORD
مطالب مشابه و مرتبط



با سلام
در فایل موجود آموزش به صورت ویدیو هست یا فقط متن؟
با تشکر
سلام.
محتویات فایل دانلود: مقاله isi، کد گمز و توضیحات در قالب WORD می باشد. ویدیو ندارد
سلام
ببخشید شما مدلسازی و حل مدل برای فصل چهارم هم انجام میدهید
سلام
بله انجام میدهیم از طریق تماس با ما در ارتباط باشید