فیلم آموزشی محاسبه نرخ ناسازگاری مقایسات زوجی روش AHP فازی و ANP فازی در اکسل
در این مطلب ابتدا روشهای AHP و ANP به صورت قطعی و فازی توضیح داده شده است سپس دو فیلم آموزشی که یکی طریقه محاسبه نرخ ناسازگاری AHP و ANP قطعی و دیگری محاسبه نرخ ناسازگاری در حالت فازی می باشد قرار داده شده است.
مقدمه
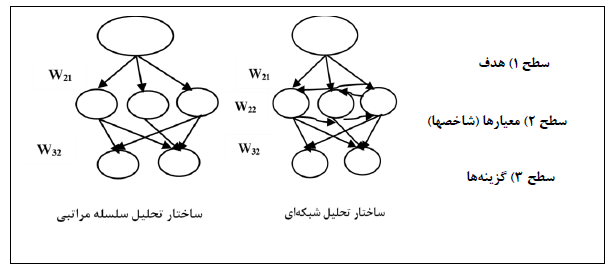
روش ahp یا فرایند سلسله مراتبی یکی از پرکاربردترین روشهای تصمیم گیری چند معیاره می باشد که توسط آقای توماس ساعتی دانشمند عراقی الاصل در سال 1980 ارائه شد و در انواع پروژه ها و مقالات مورد استفاده قرار می گیرد. پیاده سازی این روش در محیط فازی باعث حذف ابهامات موجود در تصمیم گیری می شود. روش anp فرایند تحلیل شبکه ای نیز حالت تکمیل شده ahp می باشد زیرا در حالت سلسله مراتبی ما تنها روابط از بالا به پایین را مورد بررسی قرار می دهیم اما در روش شبکه ای، علاوه بر حالت سلسله مراتبی، روابط درونی نیز مورد استفاده قرار می گیرد.
برای حل مدل های سلسله مراتبی و یا شبکه ای، ابتدا باید مقایسات زوجی در قالب یک ماتریس تشکیل شود این مقایسات زوجی بعد از پاسخگویی توسط خبرگان باید از نظر پایایی مورد بررسی قرار گیرند در روش ahp و anp نرخی بنام نرخ ناسازگاری مطرح می شود که این نرخ همواره باید از 0.1 کمتر شود این نرخ به صورت محاسبات دستی قابل محاسبه است اما دو نرم افزار سوپر دسیژن و اکسپرت چویس به راحتی این دو نرخ را محاسبه می کنند.
نکته: نرخ ناسازگاری نشان دهنده این است که آیا مقایسات ما درست بوده است یا خیر.
محاسبه نرخ ناسازگاری
یکی از گام های بسیار مهم در مدل های فرایند سلسله مراتبی و یا تحلیل شبکه ای محاسبه سازگاری مقایسات زوجی است. فرض کنید که قصد مقایسه سه خودرو رو داشته باشید اگر خودروی سمند دو برابر پژو اهمیت داشته باشید و خودروی پژو 4 برابر پراید اهمیت داشته باشد واضح است که باید خودروی سمند 8 برابر پراید اهمیت داشته باشد. این روند برای مقایسات زوجی عوامل نیز برقرار است.
تعریف 1: هرگاه شرط تعادی در ماتريس مقایسات زوحی برقرار باشد، یعنی برای تمام درایه های ماتریس A داشته باشیم:
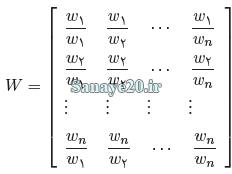
آنگاه ماتریس، سازگار نامیده می شود. ماتريس سازکار را با Ac نشان می دهیم. در حالت کلی فرض کنید w1.w2…wn شامل n وزن از پیش تعیین شده برای معیارها باشند. در این صورت ماتریس سازگار با توجه به شرط تعدی، به صورت ذیل تعریف می شود:
در نتیجه اگر A یک ماتریس سازگار باشد، آنگاه برای هر i و j داریم: aij=Wi/Wj
در صورتی که شرط تعدی برای تمام درایه ها برقرار نباشد، در این صورت ماتریس، ناسازگار بوده و میزان ناسازگاری می تواند توسط اندازه ای به نام نرخ ناسازگاری محاسبه می شود. از آنجا که مسئله ی سازگاری و ناسازگاری در مسائل چند منظوره حائز اهمیت است وجود تکنیکی که بتواند نسبت به سازگاری و ناسازگاری هر تصميم اظهارنظر کند، از اهمیت بالایی برخوردار است. یکی از مزایای مهم فرآیند تحليل سلسله مراتبی اندازه گیری و کنترل سازگاری هر ماتریس و تصمیم می باشد. به عبارت دیگر همواره در فرآیند تحلیل سلسله مراتبی میتوان میزان سازگاری تصمیم را محاسبه نمود و نسبت به خوب و بد بودن و یا قابل قبول و مردود بودن آن قضاوت کرد.
علاوه بر محاسبه ی وزن در ماتریس های ناسازگار، محاسبه ی مقدار ناسازگاری نیز از اهمیت بالایی برخوردار است. قبل از بیان معیار انداز دکیری ناسازگاری به بیان چند قضیه ی مهم می پردازیم.
برای هر ماتریس مقایسات زوجي A که مثبت و معکوس (درایه ها نسبت به قطر اصلی، معکوس هستند) است، داریم:
قضیه 1: اگر λ2، λ1 و λn مقادیر ویژه ماتریس مقایسات زوجی A باشند، آنگاه مجموع مقادیر آنها برابر n است، یعنی:
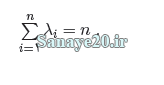
قضیه 3: اگر عناصر ماتریس مقدار کمی از حالت سازگاری فاصله بگیرد، مقادیر ویژه ی آن نیز مقدار کمی از حالت سازگاری خود فاصله خواهد گرفت.
از طرفی، طبق تعریف برای هر ماتریس مربعی A داریم:
A×W=λ×W
که در آن W و به ترتیب بردار ویژه و مقدار ویژه ی ماتریس A می باشند. در حالتی که ماتریس A سازگار باشد، یک مقدار ویژه برابر n (بزرگترین مقدار ویژه) بوده و بقیه آنها صفرند. بنابراین در این حالت می توان نوشت:
Ax W = n.W
در حالتی که ماتریس مقایسات زوجي A ناسازگار باشد، طبق قضیه ی سوم، λmax کمی از n فاصله می گیرد که می توان نوشت:
Ax W = λmax .W
پس میتوانیم نتیجه بگیریم که در هر ماتریس سازگار:
الف) مقدار وزن عناصر برابر مقدار نرمالیزه هر ستون می باشد.
ب) مقدار ویژه برابر طول ماتریس است (A x W= n . W )
پ) مقدار ناسازگاری در این ماتریس صفر است.
از آنجا که همواره λmax بزرگ تر یا مساوی n است و چنانچه ماتریس از حالت سازگاری کمی فاصله بگیرد λmax از n کمی فاصله خواهد گرفت، بنابراین تفاضل λmax و n (یعنی λmax-n ) می تواند معیار خوبی برای اندازه گیری ناسازگاری ماتریس باشد. بی تردید مقیاس λmax – n به مقدار n بستگی دارد، برای رفع این وابستگی می توان مقیاس را به صورت زیر تعریف نمود که آن را شاخص ناسازگاری
که در آن λmax بزرگترین مقدار ویژه ماتریس است و n اندازه ماتریس.
برای یک ماتریس مقایسه زوجی سازکار، λmax = n و بقیه مقادیر ویژه ماتریس برابر با صفر خواهد بود. بنابراین شاخص سازگاری در یک ماتریس سازگار برابر صفر است. هر مقدار ناسازگاری درایه های ماتریس افزایش پیدا کند مقدار λmax از n بیشتر فاصله خواهد گرفت (بزرگتر خواهد شد) و شاخص بزرگتر می شود.
برای اینکه دیدی نسبت به حدود مطلوب شاخص فرق داشته باشیم، این نسبت برای ماتریس هایی با درایه های تصادفی ولی با خواص ماتریس های مقایسات زوجی با محاسبه ی میانگین مقادیر ویژه ماتریس های مذکور توسط کامپیوتر محاسبه شده است تا شاخص ناسازگاری تصادفی (RI) را تشکیل دهد که در جدول زیر آورده شده است.
مثال محاسبه نرخ ناسازگاری
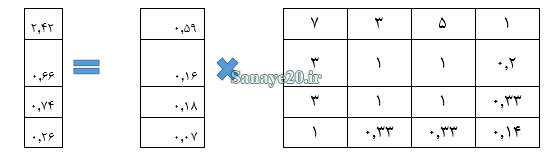
در یک مثال میخواهیم مقایسه زوجی بین 4 خودرو را تشکیل دهیم و نرخ ناسازگاری را محاسبه کنیم که بر این اساس ابتدا باید وزن را محاسبه کرد. برای محاسبه وزن کافیست که مجموع ستونی ماتریس را محاسبه کرد سپس هر عدد را تقسیم را مجموع ستونش کرد، در انتها از اعداد بدست آمده میانگین سطری گرفت که وزن بدست آید.
| مقایسه زوجی | سمند | پژو | پراید | تیبا |
| سمند | 1 | 5 | 3 | 7 |
| پژو | 0.2 | 1 | 1 | 3 |
| پراید | 0.33 | 1 | 1 | 3 |
| تیبا | 0.14 | 0.33 | 0.33 | 1 |
| مجموع ستون | 1.67 | 7.33 | 5.33 | 14 |
هر عدد ماتریس خبره یک را بر مجموع ستون تقسیم میکنیم.
| مقایسه زوجی | سمند | پژو | پراید | تیبا |
| سمند | 0.60 | 0.68 | 0.56 | 0.50 |
| پژو | 0.12 | 0.14 | 0.19 | 0.21 |
| پراید | 0.20 | 0.14 | 0.19 | 0.21 |
| تیبا | 0.08 | 0.05 | 0.06 | 0.07 |
وزن معیارها به صورت زیر محاسبه میشود. به بیان دیگر وزن برابر با میانگین حسابی درایه های هر سطر ماتریس بالا می باشد.
سپس ماتریس اولیه تصمیم را در وزن معیارها به صورت ماتریسی ضرب میکنیم:
برای محاسبه مقادیر لاندا نتایج ضرب بالا را در وزن متناظرش تقسیم میکنیم.
سپس میانگین بین لانداها را محاسبه میکنیم که λmax حاصل شود.
شاخص ناسازگاری از رابطه زیر بدست می آید:
شاخص ناسازگاری تصادفی نیز از جدول مربوطه بدست میآید، چون تعداد متغیرهای این مساله 4 می باشد شاخص ناسازگاری تصادفی (I.R) برابر 0.9 می باشد. در نهایت نرخ ناسازگاری این ماتریس تصمیم از رابطه زیر محاسبه می شود:
چون نرخ ناسازگاری این ماتریس تصمیم از 0.1 کمتر است پس این مقایسه زوجی مورد قبول می باشد.
در ویدیوی زیر مراحل محاسبه نرخ ناسازگاری در حالت AHP و ANP قطعی آموزش داده شده است.
نرخ ناسازگاری فازی
در حالت قبل برای مدل های قطعی گفته شد که با استفاده از دو نرم افزار می توان نرخ ناسازگاری را محاسبه نمود اما اگر محیط قطعی تبدیل به فازی شود می توان با استفاده از الگوریتم گوس و بوچر که در سال 1998 ارائه دادند برای محاسبه نرخ ناسازگاری استفاده کرد. در روش AHP فازی و یا ANP فازی ماتریس مقایسات زوجی باید سازگار باشند تا آن مقایسه زوجی قابل قبول باشد. برای محاسبه نرخ ناسازگاری ماتریس های مقایسات زوجی فازی از روش گوس و بوچر استفاده می شود.نرخ ناسازگاری یکی از پارمترهای مهم در مقایسات زوجی است این نرخ بیان می کند که آیا می توان به مقایسات اعتماد کرد یا خیر و یا اینکه مقایسات زوجی از اعتبار مناسبی برخوردار هستند یا خیر. این نرخ همواره باید از 0.1 کوچکتر باشد.
در این ویدیو روش گوس و بوچر برای محاسبه مقایسات زوجی فازی در نرم افزار اکسل EXCEL آموزش داده شده است. گوگوس و بوچر (1998) پیشنهاد دادند براي بررسی سازگاری، دو ماتريس (عدد مياني و حدود عدد فازي) از هر ماتريس فازي مشتق و سپس سازگاري هر ماتريس بر اساس روش ساعتي محاسبه شود.
در ویدیوی زیر مراحل محاسبه نرخ ناسازگاری در حالت AHP و ANP فازی آموزش داده شده است.
نکات مهم در مقایسات زوجی
1- در بسیاری از مواقع اساتید اصرار دارند که برای AHP یا ANP نیز عنوان پایایی ذکر شود چون این مدل بر اساس نرخ ناسازگاری استوار است می توان در قسمت پایایی ذکر کرد که پایایی پژوهش بر اساس نرخ ناسازگاری بررسی می شود که همواره باید از 0.1 کمتر باشد.
2- تعداد افرادی که به مقایسات زوجی پاسخ می دهند بر اساس نمونه گیری هدفمند و یا گلوله برفی انتخاب می شوند بنابراین تعداد آن ها صرفا از جهت خبرگی و در دسترس بودن سنجیده می شود و معمولا بین 10 تا 15 نفر هستند.
مطالب مشابه و مرتبط
- آموزش روش AHP فازی بهبود یافته
- آموزش روش AHP فازی چانگ (FAHP)
- روش AHP فازی میخایلو (اولویت بندی فازی)
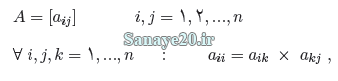
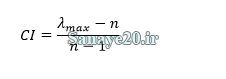



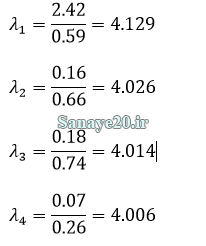
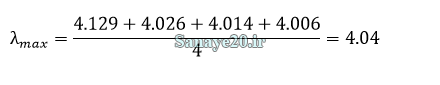
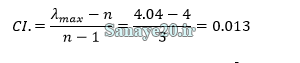
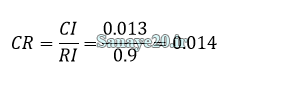

سلام وقتتون بخیر. یه سوال داشتم در مورد نرخ ناسازگاری.
وقتی نرخ ناسازگاری یک ماتریس بیشتر از ۰.۱ هست و در واقع ماتریس ناسازگار میشه. چطور میتونیم نرخ ناسازگاری رو کم کنیم و در واقع بهبود بدیم؟
سلام. اعداد مقایسه زوجی باید تغییر کنن
سلام وقت بخیر من ماتریسی دارم که 38 سطر و ستونی ( گزینه ) میشود . چگونه IR استاندارد رو به دست بیارم . ممنون میشم راهنمایی فرمایید
سلام وقت بخیر این تعداد معیار اصلا قابل مقایسه نیست
سعی کنید این 38 معیار را در چند دسته تقسیم بندی کنید