روش تبدیل تابع هدف به محدودیت
روش تبدیل تابع هدف به محدودیت از تکنیک های تصمیم گیری چند هدفه (modm) است (همانطور که قبلا گفتیم تصمیم گیری چند هدفه خود نیز بخشی از تصمیم گیری چند معیاره می باشد.) در این روش از بین توابع هدف مختلف، یکی انتخاب و سایر توابع هدف با در نظر گرفتن مقادیری، که تصمیم گیرنده یا مدل ساز تعیین می کند، به محدودیت تبدیل می شوند و مساله به یک مدل برنامه ریزی خطی یک هدفه تبدیل می شود و به طریقه معمول برنامه ریزی خطی حل می شود.
برای مثال در یک تابع دو هدفه که یکی معرفی سود و دیگری معرف میزان اشتغال باشد و تصمیم گیرنده تمایل داشته باشد میزان سود در سطح مطلوب حداقلی قرار بگیرد این تابع را با تامین حداقل نظر تصمیم گیرنده در محدودیت ها قرار می دهیم.
درصورتیکه تصمیم گیرنده مایل باشد اهداف را اولویت بندی کند در این صورت روش اولویت مطلق مطرح میشود که در این صورت مساله را نه تنها با هدفی که اولویت اول را برابر جواب بهینه بدست آمده قرار داده و به عنوان یک محدودیت به مساله اضافه کرده و مساله را با در نظر گرفتن تابه هدف با اولویت دوم حل میکنیم .
بنابراین با توضیحات ارائه شده ، در روش مربوط به اهداف حددار، تصمیم گیرنده باید بتواند قبل از حل مسئله مینیمم سطح لازم b1 از هر هدف را برای تامین شدن مشخص نماید بدین ترتیب vmp به قرار زیر خواهد بود:
تصمیم گیرنده ممکن است در این بخش ها بتواند حداقل و حداکثر لازم از سطوح هر هدف را برای تامین شدن مشخص نماید ، بدین صورت خواهیم داشت :
از مشکلات عمده این روش موارد زیر را می توان نام برد :
- مشخص نمودن b1 و u1 برای تصمیم گیرنده که اغلب منجر به محدودیت های ناسازگار و متعارض با یکدیگر میشوند.
- حتی راه حل حاصل از مدل فوق در صورت قابل حل بودن ممکن است برای تصمیم گیرنده رضایت بخش نباشد.
- اینکه کدام یک از اهداف مسئله به عنوان هدف j ام در مدل فوق برای بهینه شدن انتخاب گردد گنگ و مبهم است .
روش حددار به دلایل فوق امروز کمتر مورد استفاده قرار میگیرند.
ادغام توابع هدف در قالب یک هدف
ادغام توابع هدف چندگانه در قالب يک تابع هدف اين مزيت را دارد که مي توان در حل آن از روش هاي موجود براي حل مسائل تک هدفي استفاده نمود. البته اين کار مستلزم داشتن اطلاعات محيطي گسترده در مورد مسئله مي باشد که معمولا از ابتدا در دسترس نمي باشند.
انجام جستجو پيش از تصميم گيري اين مشکل را مرتفع مي سازد ولي در عوض از مزيت استفاده از ترجيحات تصميم گير که مي تواند فضاي جواب را کوچک کند محروم مي باشد. و بالاخره با ادغام جستجو و تصميم گيري مي توان از مزاياي هر دو دسته روش هاي فوق بهره گيري نمود.
با بازگشت به مثال اولیه همانطور که مشخص است، با جایگذاری یک هدف بجای چندین هدف مثل تابع مطلوبیت که مسئله چند بعدی اولیه را به یک مسئله تک بعدی تبدیل می کند و یا تعیین ضریب وزنی برای دو معیار سنگینی و شیرینی یک سیب، در واقع تعارضات بین معیارها را از بین بردیم و یک مسئله تصمیم گیری را به یک مسئله جستجو و تصمیم گیری تبدیل کردیم.
مسائل بهينه سازي چند هدفي يا MOP (Multiobjective Optimization Problems) کاربردهاي مختلفي در مسائل مهندسي دارند . به دلیل اینکه روشهای حل مناسبی برای مسائل چند هدفه در گذشته وجود نداشت مسائل بهینه سازی چند هدفه دارای هزینه های زیادی بودند و برای حل، آنها را به مسائل تک هدفه تبدیل می کردند.
در یک مسئله تک هدفه، تلاش ما برای بدست آوردن جوابی است که بهترین جواب از بین جواب های موجود باشد. اما در مسائل چند هدفه، بدلیل سنجش ناپذیری و وجود اهدف متضاد، ضرورتی برای وجود جوابی که از لحاظ تمام اهداف برتر از جواب های دیگر باشد وجود ندارد.
یک جواب ممکن است از لحاظ یک تابع هدف بهترین باشد اما از لحاظ تابع هدف دیگر بدترین باشد. بنابراین معمولا مجموعه ای از جواب ها برای مسائل چند هدفه وجود دارد که به راحتی با یکدیگر قابل مقایسه نیستند.
مشاهده می شود که تفاوت های اساسی زیادی بین اصول الگوریتم های حل مسائل تک هدفه و چند هدفه وجود دارد. بنابراین در ادامه ما اصول مسائل بهینه سازی چند هدفه را مورد بررسی قرار خواهیم داد.
اگر دوباره همان سبد سیب را در نظر بگیرید، با همان معیارهای وزن و شیرینی سیب. ما می توانیم انتخابمان را به مجموعه ای از سیب ها محدود کنیم که از سیب های دیگر از لحاظ هر دو معیار برتر باشند ولی خود سیب های درون مجموعه به خاطر وجود تعارضات بین اهداف، برتری نسبت به یکدیگر نداشته نباشند.
بدین صورت که اگر سیبی درون این مجموعه از سیب دیگر شیرین تر باشد، وزنش نسبت به آن سیب کمتر باشد، در واقع بهبود یک معیار باعث بدتر شدن معیار دیگر شود. به چنین جواب هایی جواب های بهینه پارتو (Pareto) ، غیر مغلوب و یا کارا گفته می شود.
تصمیم نهایی ما همیشه یکی از این سیب های غیر مغلوب است. رویکرد پارتو فرض می کند که هیچ آگاهی نسبت به برتری توابع هدف نسبت به یکدیگر وجود ندارد. در ادامه چند تعریف در این رابطه آورده می شود.
ساختار و پیچیدگی مسائل چندهدفه
بطور کلی، مسائل بهینه سازی چند هدفه از پیچیدگی زیادی برخوردارند. دو نوع سختی در حل این مسائل وجود دارد که بایستی تفکیک شوند:
- سختی ذاتی مسئله
- سختی های مرتبط با تکنیک ها حل.
اصلی ترین مانع روش های موجود آنست که آنها بسیار حساس و وابسته به مقادیر وزن ها، یا الویت از پیش تعیین شده اهداف و یا شکل تابع مطلوبیت هستند. ماهیت این دشواری ها مربوط به تکنیک های حل است نه سختی خود مسئله.
بطورکلی، یک مسئله بهینه سازی چند هدفه توسط ساختار و مشخصاتی که در ادامه بیان میکنیم شناخته میشود:
- توابع هدف و فضای اهداف
- توابع محدودیت و فضای جواب
- اندازه مسئله
توابع هدف و محدودیت ها می توانند خطی یا غیر خطی; محدب، مقعر، یا همچنین; مشتق پذیر یا غیر قابل مشتقگیری; پیوسته یا نیمه پیوسته; تک قله ای یا چند قله ای باشند. به همین ترتیب معیار ها و فضای جواب نیز میتواند محدب یا غیر محدب، بهم پیوسته یا غیر بهم پیوسته، پیوسته یا گسسته باشد.
اندازه مسئله نیز بر اساس تعداد متغیرهای تصمیم، محدودیت ها و اهداف بدست می آید. اصلی ترین رویکردهای مرسوم محدود به توابع خطی و فضای جواب محدب هستند.
در اینجا سعی کردیم روش تبدیل تابع هدف به محدودیت را با ارائه مثالها و توضیحات جامع شرح دهیم. آیا تا بحال از این روش استفاده کرده اید؟ اگر تجربه ای در این زمینه دارید در بخش زیر با ما به اشتراک بگذارید و همچنین می توانید نظرات و سوالات خود را برای ما ارسال کنید.


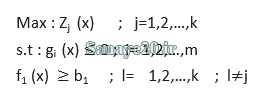
سلام وقت بخیر دقیق من این قسمت لازم دارم ازکدوم قسمت سایت میتونم تهیه اش کنم
سلام آموزشی ازش نداریم