مدل برنامه ریزی آرمانی برای تکنیک BWM
مقدمه
روش بهترین بدترین (BWM) یک روش تصمیم گیری چند معیاره می باشد که بر اساس سیستم مقایسات زوجی بنا شده است. بکارگیری یک چنین رویکرد سیستماتیک مقایسات زوجی، باعث افزایش سازگاری و قابلیت اطمینان نتایج می شود. روش BWM زمانی که دو یا سه معیار داریم و یا زمانی که سازگاری کامل برقرار است برای هر تعداد معیار، همواره جواب منحصربفردی را ارائه می کند. اما در مسائلی که سازگاری کامل برقرار نیست و بیش از سه معیار وجود دارد، ممکن است جواب بهینه چندگانه داشته باشیم. داشتن جواب بهینه چندگانه در اغلب موارد، مطلوب تصمیم گیرندگان نیست. روش آرمانی BWM قادر است جواب منحصربفرد ارائه نماید. همچنین با کاهش تعداد محدودیت ها نسبت به مدل اصلی، محاسبات را بسیار ساده تر کرده است. روش برنامه ریزی آرمانی همواره به دنبال حداقل کردن انحرافات از هدف می باشد.
در سال های اخیر ، روش های تصمیم گیری چند معیاره (MCDM) توسط بسیاری از محققان توسعه یافته و برای بسیاری از مسائل در دنیای واقعی اعمال شده است. MCDM را می توان در تصمیم گیری به دو دسته طبقه بندی کرد: MADM برای ارزیابی و MODM برای طراحی می باشد. در MADM ، گزینه های دیگر از پیش تعریف شده اند. با این حال ، MODM با در نظر گرفتن محدودیت های مختلف بهترین گزینه را طراحی می کند.این روشها در حال حاضر روشهای نرمال ومعمولی هستند که بیشترین استفاده را دارند.معمولا انتخاب روشهای دیگر با خطا و مشکل مواجه میشود و کاربران ترجیح میدهند که از روشهای موجود انتخاب کنند.
روش BWM
این تکنیک یک روش MADM است که بر اساس یک سیستم مقایسه زوجی کار می کند. مهمترین مزایای تکنیک BWM به شرح زیر است: (1) به مقایسات زوجی کمتری نیاز دارد. (2) منجر به سازگاری بیشتر می شود. بنابراین ، BWM نتایج قابل اطمینان تری را ارائه می دهد. در این روش ، تصمیم گیرنده بهترین (مطلوب ترین) و بدترین (کمترین مطلوبیت) معیار را مشخص می کند. سپس مقایسات زوجی باید بین هر یک از این معیارها (بهترین و بدترین) و سایر معیارها بدست آید.
رضایی (2016) تجزیه و تحلیل بازه ای را برای چندین راه حل بهینه جهت سیستم های مقایسه ای کاملاً سازگار و زمانی که مساله بیش از سه معیار دارد ارائه داد. او همچنین یک مدل خطی از BWM را پیشنهاد کرد. تفاوت اصلی بین BWM و سایر روش ها مبتنی بر مقایسه زوجی این است که این روش ها از ماتریس مقایسه زوجی استفاده می کنند (رابطه 1) در حالی که BWM از بردارهای مقایسه زوجی استفاده می کند (PCV) که در رابطه 2 مشخص شده است.
اخیراً، استفاده از برخی از روشهای مبتنی بر مقایسه زوجی توجه بیشتری را به خود جلب کرده است، زیرا محاسبه نرخ سازگاری در آن باعث بررسی اطمینان در مقایسه زوجی می شود و این باعث افزایش قابلیت اطمینان نتایج می شود. با این حال، محققان به دلیل تعداد زیاد مقایسه ها و همچنین نسبت سازگاری نامناسب در ماتریس های مقایسه زوجی بزرگ، مشکلات مختلفی روبرو بوده اند. BWM توسط رضایی (2015) پیشنهاد شد تا یک سیستم مقایسه زوجی دقیق با تعداد کمتر داشته باشد. علاوه بر امکان محاسبه نرخ سازگاری، BWM تعداد مقایسه ها را به 2n-3 کاهش می دهد و باعث می شود نسبت سازگاری بهتر و دقت نتایج حاصل شود.
پیشینه پژوهش مدل BWM
تاکنون ، برخی از محققان تلاش کرده اند BWM را در محیط فازی توسعه دهند. گو و زو (2017)، BWM را به محیط فازی گسترش داده و آن را با BWM مقایسه کردند. لو و لیو (2018)، یک مدل ترکیبی را برای حالت خرابی و تجزیه و تحلیل اثر ارائه دادند. این مطالعه مدل BWM را با توجه به FBWM اصلاح می کند که توسط گو و زو (2017) ارائه شده است.
برخی از محققان تلاش کردند تا پایه BWM را بر اساس اعداد راف (rough) ایجاد کنند و برخی از محققان BWM راف (rough) را در مطالعات خود اعمال کردند. زاوادکس (2018) رویکرد SWARA راف را توسعه داد و نتیجه بدست آمده را با BWM راف و AHP راف مقایسه کرد تا مقادیر وزن را تعیین کند. نتایج نشان داد که همبستگی رتبه های با استفاده از SWARA راف با رتبه های BWM راف و AHP راف کامل است
مدل آرمانی BWM
همانطور که قبلاً نیز گفته شد، مدل BWM برای سیستم های مقایسه ای کاملاً سازگار با بیش از سه معیار، ممکن است منجر به راه حل های بهینه چندگانه شود. این بدان معناست که در یک مساله ممکن است چندین وزن بهینه ایحاد شود. اگرچه ممکن است در بعضی موارد بهینه چندگانه مطلوب باشد، در موارد دیگر، DM ها (تصمیم گیرنده ها) ترجیح می دهند یک راه حل منحصر به فرد داشته باشند، در اینجا به توضیح مدل BWM آرمانی که توسط Amiri & Emamat (2020) ارائه شد پرداخته می شود در این بخش دو مدل پیشنهاد می کنیم که راه حل بهینه منحصر به فرد را تضمین می کنند. مدلهای پیشنهادی از متغیرهای آزاد در علامت زیر استفاده کرده و قدر مطلق را در محدودیت ها از بین می برند.
این مدل ها دارای تعداد 2n-2 محدودیت هستند در حالی که مدل های قبلی دارای 4n-5 محدودیت بودند. بنابراین، مدلهای پیشنهادی در مقایسه با مدلهای قبلی محدودیت کمتری دارند، که منجر به پیچیدگی محاسباتی کمتری می شود. می توان گفت که تعداد محدودیتها در مدلهای ارائه شده بطور چشمگیری کاهش یافته است.
در مدل غیرخطی اگر Wi/Wj=aij رابطه برقرار باشد مدل سازگاری کامل دارد اما در دنیای واقعی همواره ناسازگاری هایی وجود دارد بر این اساس مقدار ناسازگاری برای مقایسات بهترین معیار با دیگر معیارها توسط رابطه 1 و مقدار ناسازگاری برای مقایسه دیگر معیارها با بدترین معیار توسط رابطه 2 منعکس شده است.
تابع هدف این مدل مینیمم سازی انحرافات کل می باشد بنابراین مدل غیر خطی روش BWM آرمانی در زیر آورده شده است.
در مدلهای بهینه سازی همواره مدل خطی بر مدل غیرخطی ارجحیت دارد در این روش نیز تبدیل مدل غیرخطی به خطی نیز حائز اهمیت می باشد بنابراین مدل خطی این روش به صورت زیر می باشد. در این مدل اگر Wi=aij*Wj باشد سازگاری کامل می باشد.
نرخ سازگاری در مدل BWM آرمانی
نرخ سازگاری نشان دهنده این است که مقایسات انجام شده تا چه میزان قابل اعتماد است و نتیجه درستی ایجاد می کند در مدل bwm آرمانی بر اساس رابطه زیر این نرخ محاسبه می شود هر چه این نرخ به صفر نزدیکتر باشد نشان از سازگاری بیشتر مقایسه زوجی دارد.
مطالب مشابه و مرتبط




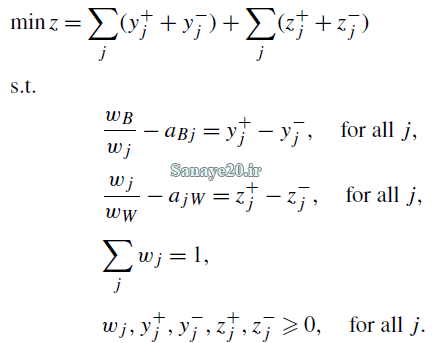
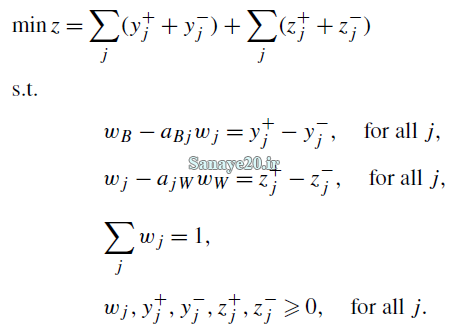
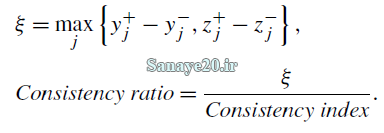
سلام ممنون از مطالب خوب و کاربردی که در سایت قرار دادید
آبا روش های وزن دهی جدیدتری ارایه شده است در سال 2022؟
سلام وقت بخیر. طبق بررسی هایی که داشتم هنوز خیر. بیشتر روشهایی که ارائه میشه تکنیک های گزینه محور و رتبه بندی گزینه هستند